富阪幸治(国立天文台)天文月報2000年10月号
要約
星間雲から星への進化について主に理論的な立場から理解の現状をまとめてみる。そのなかで、磁場の役割(準臨界雲、超臨界雲)、双極性分散(ambipolar diffusion)、収縮を記述するLarson-Penston解、Shu解が進化のどのような相に登場するのかをまとめる。また、星形成領域にみられる双極分子流や光学ジェットなどのアウトフロー現象がいつ形成され、星形成でどのような役割を果たしているかを概観する。
1.はじめに
星間雲から星への収縮の道筋を明らかにすることは宇宙物理学の基本的な問題であり続けてきた。そこには、星の持つ基本的な物理量、質量、角運動量、磁束などが、その母体である星間分子雲コアの物理状態とどんな関係になっているのかを知りたいという問題が存在してきた。ここでは、主にシミュレーションを用いた理論的立場から星間雲から星への収縮の道筋がどこまで理解されているのかを述べてみることにする。
2.ビリアル解析
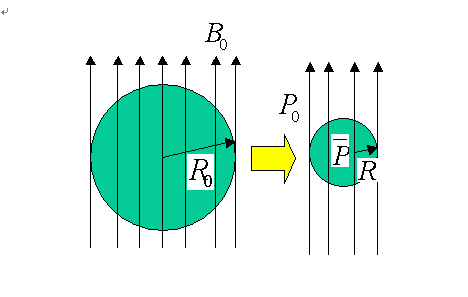
星形成の母体と考えられている星間分子雲あるいはその中の特に密度の高い部分である分子雲コアはどのような状態にあるのだろうか。それは、普段に変化し静的ではないとも考えられるが、まず、力学的な釣り合いにあるとしたらどのような状態にあるかを考えておく。図1のような状況を考え、ビリアル関係式(付章A2式)で![]() とすると、力学的釣り合い(力学平衡)が成り立つための条件が得られる。
とすると、力学的釣り合い(力学平衡)が成り立つための条件が得られる。
自己重力に抗して熱圧力で支えられる最大質量をジーンズ質量という。これを求めてみよう。磁場の項を0とすると
![]() (1)
(1)
となるが、星間雲の密度(![]() )でよく成り立つ等温の仮定をすると、内部の平均圧力
)でよく成り立つ等温の仮定をすると、内部の平均圧力![]() は質量M、平衡の半径R、等温音速csを使って
は質量M、平衡の半径R、等温音速csを使って
![]() (2)
(2)
と書けるので、星間雲の表面にかかっている外圧P0は質量M、平衡の半径Rと次のような関係を持つことがわかる:
![]() (3)
(3)
質量Mを一定にしておき、釣り合う半径Rを0から増加させると外圧P0は初め増加するが、あるところで最大値 ![]() を持ち、減少することがわかる。これは質量Mの球状の釣り合い状態が可能なためには表面にかかっている圧力に上限があることを示している。反対にいうと、ある外圧P0下に置かれた球対称の等温気体が力学的な釣り合いをとれるためには質量Mに上限があることを意味している。これは通常ジーンズ質量と呼ばれ、
を持ち、減少することがわかる。これは質量Mの球状の釣り合い状態が可能なためには表面にかかっている圧力に上限があることを示している。反対にいうと、ある外圧P0下に置かれた球対称の等温気体が力学的な釣り合いをとれるためには質量Mに上限があることを意味している。これは通常ジーンズ質量と呼ばれ、
![]() (4)
(4)
のように表される(簡単にするために係数aの値は1にした)。外圧を考慮して密度は![]() であるべきだとして、密度分布をうち切ったLane-Emden方程式を用いて星間雲の内部の密度分布も考慮したBonnor(1955)とEbert(1956)の計算によると係数の値が少し異なり
であるべきだとして、密度分布をうち切ったLane-Emden方程式を用いて星間雲の内部の密度分布も考慮したBonnor(1955)とEbert(1956)の計算によると係数の値が少し異なり![]() となる(これはBonnor-
Ebert質量と呼ばれる)。
となる(これはBonnor-
Ebert質量と呼ばれる)。
2.2磁気的超臨界雲と準臨界雲
式(1)で考慮しなかった磁場による効果を取り入れることによって磁場のローレンツ力も込みで力学的な釣り合いを保つことのできる最大の質量(臨界質量)を見積もることができる。
式(A1)の磁場の項は、星間雲を貫く磁束が一定![]() である場合は(A4)の様に、釣り合いの半径に反比例することがわかる。同じようにRに反比例する自己重力の項と一緒にすると、平衡の式は
である場合は(A4)の様に、釣り合いの半径に反比例することがわかる。同じようにRに反比例する自己重力の項と一緒にすると、平衡の式は
![]() (5)
(5)
のようになる。ここで![]() は星間雲を貫く磁束に比例し
は星間雲を貫く磁束に比例し![]() となるように決めた。
となるように決めた。
これから、釣り合いに与える磁場の効果について次のようなことがわかる。(1)磁場は星間雲の質量が減少したかのような効果を持つ。しかし、(2)収縮が進んでRが減少し磁気圧や磁気張力が増したからといって、磁場が重力に対して優勢になることはない。
(5)式で![]() の場合は、最後の重力の項が正になるので、外圧
の場合は、最後の重力の項が正になるので、外圧![]() の値に関わらず、釣り合いの半径
の値に関わらず、釣り合いの半径![]() の値が存在する。反対に
の値が存在する。反対に![]() の場合は、磁場のない場合と同じで外圧
の場合は、磁場のない場合と同じで外圧![]() には力学平衡が成り立つために上限が存在する。従って、
には力学平衡が成り立つために上限が存在する。従って、![]() が磁場が力学釣り合いに非常によく効くかどうかの質量の基準を与える。この臨界的な質量と磁束の比の値は、より現実的な軸対称(球ではなく)の磁気流体的平衡形状の計算(Tomisaka
et al. 1988)から
が磁場が力学釣り合いに非常によく効くかどうかの質量の基準を与える。この臨界的な質量と磁束の比の値は、より現実的な軸対称(球ではなく)の磁気流体的平衡形状の計算(Tomisaka
et al. 1988)から
![]() (6)
(6)
と見積もられている。通常、質量が磁束で決まるこの臨界質量よりも軽く、どのような外圧の元でも力学的釣り合いを持つようなものを磁気的準臨界雲と呼び、この質量より重く、外圧によっては力学釣り合いを持たないものを磁気的超臨界雲と呼んでいる。![]() の場合の、この外圧の条件は、磁場を持った星間雲のジーンズ質量に相当するもの(Mmag)が存在することを意味しており、磁気流体的平衡形状の計算結果からは、
の場合の、この外圧の条件は、磁場を持った星間雲のジーンズ質量に相当するもの(Mmag)が存在することを意味しており、磁気流体的平衡形状の計算結果からは、
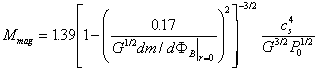 (7)
(7)
でよく表されることが知られている(Mouschovias & Spitzer 1976及びTomisaka et al. 1988)。したがって、力学的釣り合いにあるための条件は
![]() (8)
(8)
で与えられることになる。このMmagのことを臨界質量と呼ぶこともある。
これらの質量はどれくらいになるのだろうか。星間雲の内部の温度を10K、表面での密度を100cm-3とする(外圧は103Kcm-3)として、ジーンズ質量を見積もると、10-20M?程度になる。また、磁気的な臨界質量は半径0.2pc程度の分子雲コアを100μG程度の磁場が貫いている場合は、50M?程度になる。
3.進化の道筋
それでは、質量が異なる星間雲の進化はどのように異なるのだろうか。次の4節で詳しく述べるが、不安定性などによって平衡状態を持たないM>Mmagの星間雲が形成された場合は、その星間雲は自由落下時間程度で収縮すると考えられる。そして、ガスの状態方程式が等温である限りその収縮は止められないことがわかる(回転運動があり遠心力が働くと、ビリアル定理の範囲内では収縮が止まるはずあるが、後に述べるように暴走的収縮の間は収縮が止まることはない。これは5節に詳しく述べる)。それに対して、M<Mmagの星間雲の場合は、力学的釣り合い状態をもちえる。しかしこのような電離度の低い分子雲の内部ではイオンや電子は磁場と結合しているが、中性の分子はローレンツ力を直接受けることはできず、分子はイオンとの衝突を通じて運動量をやりとりし、磁場と結合しているイオンと同じように運動しようとする形で間接的にだけ磁場と結合している。このような状況では、中性粒子は電離粒子に対して中心に落下する方向に有限の速度差(超臨界雲をシミュレーションしたときにみられる超音速の落下速度に比べて十分小さい。速度差に比例した運動量の交換を行う)を持つことになり、その結果として磁束に対しても中性粒子はゆっくりと落下することになる。中性ガスからみると磁束が外に逃げ出すことになる。この現象を双極的分散(ambipolar diffusion)と呼んでいる。これによって、中心部の質量/磁束比が次第に増加する。その結果、式(7)からもわかるように、中心部の質量/自磁束比の減少関数である力学的釣り合い可能な最大質量Mmagが減少する。そして、これが実際の質量を下回るともはや力学的な釣り合いは不可能になり、M>Mmagの星間雲とおなじ動的な進化を起こすと考えられている(Nakano 1979)。そしてこの進化の時間は動的収縮の場合よりもゆっくりでほぼ自由落下時間の10倍程度と見積もられている。
ここで重要なことは、星間雲から星への進化の過程で過剰になる星間磁場(磁束)がいつ星あるいは分子雲コアから流出するかという、「星の磁束問題」に関連した以下の事実である。つまり軸対称2次元の計算では、中心部で起こる磁束の流出言い換えれば![]() の上昇は中心の密度が
の上昇は中心の密度が![]() 程度のかなり高密度に達しなければ大きくはならないという結果が得られているという点である。
程度のかなり高密度に達しなければ大きくはならないという結果が得られているという点である。![]() の値は中心で何倍かにしかならなくても、星間雲の中心部の構造は大きく変化し、密度は何桁も変化するのである(Nakano
1979)。これに対して、板状の星間雲がそれに平行な磁場を持っている場合のMouschoviasら(1985)の計算では、収縮する過程で、
の値は中心で何倍かにしかならなくても、星間雲の中心部の構造は大きく変化し、密度は何桁も変化するのである(Nakano
1979)。これに対して、板状の星間雲がそれに平行な磁場を持っている場合のMouschoviasら(1985)の計算では、収縮する過程で、![]() 程度の分子雲コアの密度から、密度上昇とともに、密度ρ/磁束密度B比が大きく変化することが予測された。この2人の間では活発な論争が行われたが、現在ではこの結果の違いは、問題の対称性あるいは次元の違いによっていると考えられている。つまり平衡平板の系では、面密度σと中心密度ρcは
程度の分子雲コアの密度から、密度上昇とともに、密度ρ/磁束密度B比が大きく変化することが予測された。この2人の間では活発な論争が行われたが、現在ではこの結果の違いは、問題の対称性あるいは次元の違いによっていると考えられている。つまり平衡平板の系では、面密度σと中心密度ρcは![]() という関係がなりたつので、密度ρさえあげれば磁場がなくともいくらでも面密度を増やせるのに対して、球や軸対称の系では、中心密度ρcを増加させても支えられる質量には上限があるため平衡平板の系のようなことはおこならいと考えればよい。
という関係がなりたつので、密度ρさえあげれば磁場がなくともいくらでも面密度を増やせるのに対して、球や軸対称の系では、中心密度ρcを増加させても支えられる質量には上限があるため平衡平板の系のようなことはおこならいと考えればよい。
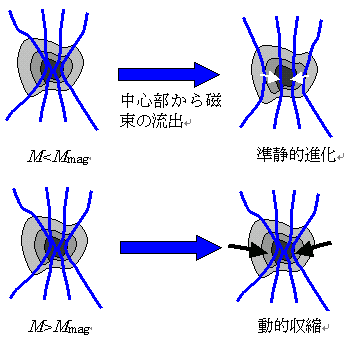 図2準臨界雲(上)と超臨界雲(下)の進化の違い
図2準臨界雲(上)と超臨界雲(下)の進化の違い
前節で見たように、力学釣り合いにある星間雲は双極的分散過程によって中心の密度が上昇し、質量/磁束比が力学釣り合いを許す値の範囲を越えると動的な収縮に移行すると考えられている。また、初めから力学釣り合いにない重い星間雲は形成後早い時期に動的収縮を開始する。
1969年に初期に力学的釣り合いからはずれた一様密度の球対称の等温星間雲の収縮がLarsonとPenstonによって調べられた。それによると初期の半径を音速で横切る程度の時間が経過すると収縮は「自己相似的」に進行する。解は中心から![]() 程度の空間的に一定の密度
程度の空間的に一定の密度![]() をもつ平坦部分と、その外の密度が中心からの距離の2乗に反比例(
をもつ平坦部分と、その外の密度が中心からの距離の2乗に反比例(![]() )する部分に分けられ、平坦部分では落下速度は中心からの距離にほぼ比例し、一方、外側の密度が距離の2乗に反比例して減少する部分では、落下速度は音速の3倍程度でほぼ一定になるという性質を持つことがわかった。そして、時間が経過し中心密度の上昇した時の解は、以前の中心密度の低い解を、中心からの距離を縮小し、中心密度を増加させるように、横軸縦軸とも何倍かすることによって得られるという性質を持つことがわかっている。このような性質を自己相似とよぶ。そして、中心密度が1桁上昇するために必要な時間は自由落下時間
)する部分に分けられ、平坦部分では落下速度は中心からの距離にほぼ比例し、一方、外側の密度が距離の2乗に反比例して減少する部分では、落下速度は音速の3倍程度でほぼ一定になるという性質を持つことがわかった。そして、時間が経過し中心密度の上昇した時の解は、以前の中心密度の低い解を、中心からの距離を縮小し、中心密度を増加させるように、横軸縦軸とも何倍かすることによって得られるという性質を持つことがわかっている。このような性質を自己相似とよぶ。そして、中心密度が1桁上昇するために必要な時間は自由落下時間![]() に比例し、それは中心密度の1/2乗に反比例して短くなり、有限の時間で中心密度は無限に上昇する。
に比例し、それは中心密度の1/2乗に反比例して短くなり、有限の時間で中心密度は無限に上昇する。
図3(Whitworth &
Summers 1985)にLarson-Penstonによる自己相似解を破線から実線につながる一連の解で示してある。
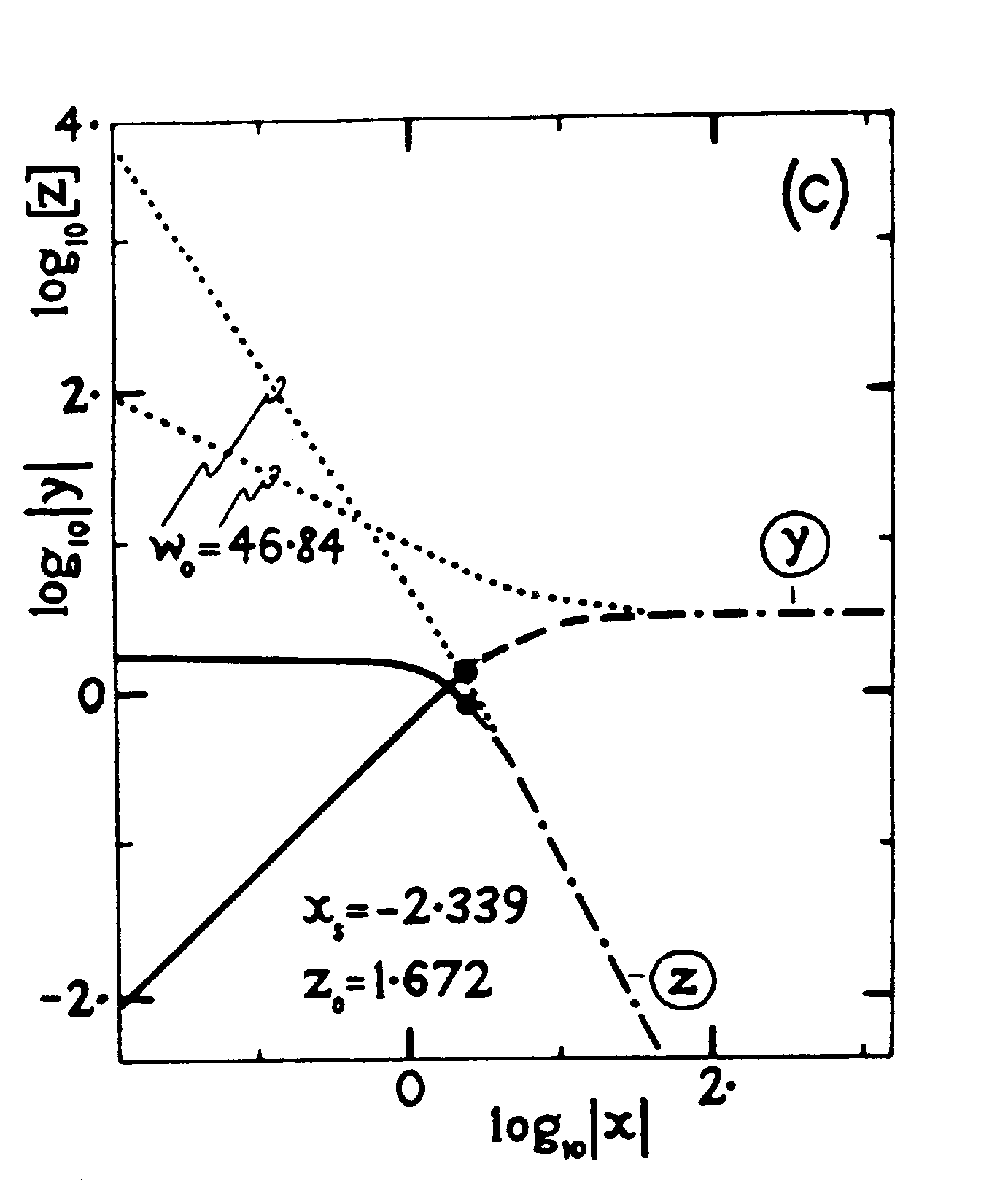 図3:コア形成以前の暴走的収縮を表す自己相似解とコア形成以降の降着を伴う自己相似解(Whitworth
& Summers 1985より)。
図3:コア形成以前の暴走的収縮を表す自己相似解とコア形成以降の降着を伴う自己相似解(Whitworth
& Summers 1985より)。![]() は相似座標、yは密度、zは落下速度に対応する無次元量。どちらも外側で一致し中心部で異なる二つの解(実線:暴走的収縮、点線:降着解)が示されている。
は相似座標、yは密度、zは落下速度に対応する無次元量。どちらも外側で一致し中心部で異なる二つの解(実線:暴走的収縮、点線:降着解)が示されている。
ここでzは密度分布、yは落下速度分布を表す。なお横軸は![]() (τは収縮が進み密度が発散するときまでの時間を表す)である。力学釣り合いを達成できないような重い星間雲の場合は(特に中心部分では)この解が実現すると考えられる。
(τは収縮が進み密度が発散するときまでの時間を表す)である。力学釣り合いを達成できないような重い星間雲の場合は(特に中心部分では)この解が実現すると考えられる。
Larsonは、さらに進化の進んだ状態についても計算を行った。中心部で密度がおよそ![]() に達すると、それまでガスを冷却して等温に保ってきたダストからの熱輻射に対して中心部が光学的に厚くなり、中心部で水素分子ガスは断熱的になる。こうして、中心部で収縮がいったん止まりほぼ力学的に釣り合ったコアを形成する(第1コア)。外部からの降着によって質量が増えるため中心密度を増加させながらゆっくりと収縮が進む。中心密度が
に達すると、それまでガスを冷却して等温に保ってきたダストからの熱輻射に対して中心部が光学的に厚くなり、中心部で水素分子ガスは断熱的になる。こうして、中心部で収縮がいったん止まりほぼ力学的に釣り合ったコアを形成する(第1コア)。外部からの降着によって質量が増えるため中心密度を増加させながらゆっくりと収縮が進む。中心密度が![]() に達すると断熱圧縮によって温度は
に達すると断熱圧縮によって温度は![]() まで上昇し、水素分子の解離が起こる(中心部で温度と密度がどのように変わるかは図 4を参照のこと)。この反応は吸熱反応なので圧縮によって気体にされた仕事は解離に使われ温度上昇はいったん緩やかになる。ポリトロープ指数(
まで上昇し、水素分子の解離が起こる(中心部で温度と密度がどのように変わるかは図 4を参照のこと)。この反応は吸熱反応なので圧縮によって気体にされた仕事は解離に使われ温度上昇はいったん緩やかになる。ポリトロープ指数(![]() )は1.1に減少する(この値は球対称の計算から得られたもので、圧縮による加熱と解離に伴う吸熱反応の差し引きによって決まっている)。そのため、コアは収縮することができるようになり暴走的収縮が再び実現する。これを第2収縮と呼ぶ。状態方程式が再び断熱的になるのは解離が終了し組成が水素原子主体になった後である。ここで再び形成されるコアを第2コアと呼び将来星になる部分ができたことになる。
)は1.1に減少する(この値は球対称の計算から得られたもので、圧縮による加熱と解離に伴う吸熱反応の差し引きによって決まっている)。そのため、コアは収縮することができるようになり暴走的収縮が再び実現する。これを第2収縮と呼ぶ。状態方程式が再び断熱的になるのは解離が終了し組成が水素原子主体になった後である。ここで再び形成されるコアを第2コアと呼び将来星になる部分ができたことになる。
一方、力学的釣り合いを保ちながら双極的分散でゆっくりと中心密度を上昇させてきた星間雲が経験する動的収縮を表す球対称な解として、Shu(1977)はインサイド−アウト(inside-out)収縮という解を提案した。ちなみにinside-outとは靴下を表裏さかさまに履くような状態をいい、ある種のかけことばになっている。かれは、初期に、中心では密度が発散するが力学的釣り合い(v=0)にある![]() という密度分布を考え、これを双極的分散で到達する最終状態と考えた。その後、中心に無限小の質量の第1コアが形成されると、そこに向かって等温ガスの降着が起こる。この場合は降着が始まってからτが経過すると、中心から
という密度分布を考え、これを双極的分散で到達する最終状態と考えた。その後、中心に無限小の質量の第1コアが形成されると、そこに向かって等温ガスの降着が起こる。この場合は降着が始まってからτが経過すると、中心から![]() の部分にまで降着流が発達し、その落下速度は
の部分にまで降着流が発達し、その落下速度は![]() (ここでMrはrより内側に存在する全質量で、極初期を除いて中心のコアの質量と考えればよい)、また密度分布はほぼ時間的に一定の中心のコアへの質量降着率
(ここでMrはrより内側に存在する全質量で、極初期を除いて中心のコアの質量と考えればよい)、また密度分布はほぼ時間的に一定の中心のコアへの質量降着率![]() を使って、
を使って、![]() のようになる。
のようになる。
Shuのインサイド−アウト解では中心と外側で密度分布が
![]() (9)
(9)
のようになるが、Larson-Penstonの暴走的収縮解では
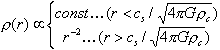 (10)
(10)
を予想するから、密度分布の![]() からずれた内側の指数を観測的に決めることができれば、どちらの解が成り立っているかを決めることができ、ひいては母体となった星間雲(あるいは分子雲コア)が力学的釣り合いにあったかどうかを決めることができると考えるのはもっともなことである。その線に沿ったZZZやZZZの観測からは-3/2乗に近い指数が得られるという報告もある。
からずれた内側の指数を観測的に決めることができれば、どちらの解が成り立っているかを決めることができ、ひいては母体となった星間雲(あるいは分子雲コア)が力学的釣り合いにあったかどうかを決めることができると考えるのはもっともなことである。その線に沿ったZZZやZZZの観測からは-3/2乗に近い指数が得られるという報告もある。
しかし、この比較は、LarsonとPenstonが調べた第1コア形成前の解と第1コア形成後に成り立つインサイド−アウト解を比較していることになっている。Larson-Penston解の第1コア形成後の解はどのようになっているのだろうか。これに対する答えは、Whitworth
& Summers (1985)によって自己相似解の形で得られていて、図3の点線のようになている。彼らは、外部でLarson-Penston解のコア形成前の解に漸近し、内側で降着を示す解を見つけた。コア形成前の解では中心に近づくときに密度は![]() と有限に留まり、落下速度も
と有限に留まり、落下速度も![]() に漸近しなければならないが、コア形成後には降着率
に漸近しなければならないが、コア形成後には降着率![]() が有限になっていれば、落下速度も密度も中心に向かって大きくなっていてもよい。このLarson-Penston解のコア形成後の解もインサイド−アウト解と同じく、中心付近で密度が距離の3/2乗に反比例
が有限になっていれば、落下速度も密度も中心に向かって大きくなっていてもよい。このLarson-Penston解のコア形成後の解もインサイド−アウト解と同じく、中心付近で密度が距離の3/2乗に反比例![]() し、落下速度が
し、落下速度が![]() という性質を示す。またインサイド−アウト解と同様に、このべき分布を持つ部分は、コア形成時点からの時間τとともに外側に広がってゆく。初期に力学的釣り合いにあり静止しているインサイド−アウト解では内側の落下を示しているのは
という性質を示す。またインサイド−アウト解と同様に、このべき分布を持つ部分は、コア形成時点からの時間τとともに外側に広がってゆく。初期に力学的釣り合いにあり静止しているインサイド−アウト解では内側の落下を示しているのは![]() の部分だけで、それより外の部分は静止しているのに対して、コア形成後のL-P解は
の部分だけで、それより外の部分は静止しているのに対して、コア形成後のL-P解は![]() 程度で落下しているという点で違いがある。ただ、ここで注意しておきたいことは、インサイド−アウト解では、落下する部分は希薄波(rarefaction
wave)で、静止している部分との境界が希薄波の先頭で、これが音速で外に向かって伝搬する。一方コア形成前のL-P解は落下速度が超音速であるから、音速で伝わる「中心でコアが形成した」という情報は外向きには伝搬できない。それでは、なにが解の性格を変えさせるかというと、中心に点源のコアが形成されたことによって中心近くで感じる重力場が変化することによる。どう変わるかというと、コア形成前にはローカルな密度分布(圧力分布にも比例)を内側に外挿して得られる質量からの重力だけだったものが、それにコアからの点源の重力が加わるのである。
程度で落下しているという点で違いがある。ただ、ここで注意しておきたいことは、インサイド−アウト解では、落下する部分は希薄波(rarefaction
wave)で、静止している部分との境界が希薄波の先頭で、これが音速で外に向かって伝搬する。一方コア形成前のL-P解は落下速度が超音速であるから、音速で伝わる「中心でコアが形成した」という情報は外向きには伝搬できない。それでは、なにが解の性格を変えさせるかというと、中心に点源のコアが形成されたことによって中心近くで感じる重力場が変化することによる。どう変わるかというと、コア形成前にはローカルな密度分布(圧力分布にも比例)を内側に外挿して得られる質量からの重力だけだったものが、それにコアからの点源の重力が加わるのである。
ともあれ、密度分布の![]() からずれた内側の指数を観測的に決めることから、L-P解とインサイド−アウト解のどちらが成り立つかを決めるという問題は、コア形成後のL-P解がインサイド−アウト解とにているためにすくなくともコア形成後については容易でないと思われる。
からずれた内側の指数を観測的に決めることから、L-P解とインサイド−アウト解のどちらが成り立つかを決めるという問題は、コア形成後のL-P解がインサイド−アウト解とにているためにすくなくともコア形成後については容易でないと思われる。
5.回転とアウトフロー
ここまで見てきた話には星間雲の持つ回転運動の効果は考えに入れてこなかった。しかし分子雲コアに観測される数km/sにおよぶ視線速度の勾配が回転運動を表しているとすると分子雲コアの持つ比角運動量は
![]() (11)
(11)
に達する(ここではコアは半径Rの一様密度の球が一様回転しているものと仮定した)。これはたとえば距離100AUだけ離れた1太陽質量の連星系の軌道角運動量
![]() (12)
(12)
に比べてもかなり大きい値であるし、前主系列星であるT Tau型星の持つ典型的なスピン比角運動量
![]() (13)
(13)
(ここでPは回転周期、R*はT
Tau型星の半径であり、星は一様密度の球と仮定した。)と比べれば非常に大きな値である。つまり、星間分子雲コアが持っていた角運動量はその進化に大きな役割を果たしたと考えられる。さらにいうと、もし星間分子雲コアが持っていた角運動量が保存されていれば、遠心力釣り合い半径
![]()
(14)
で重力と遠心力が釣り合ってそれ以上の収縮は起こらなかったはずであるといえる。角運動量は比較的早期に分子雲コアから逃げ去ったはずである。これがどのようなプロセスによっているのかを見る前に、回転等温ガス雲の重力収縮はどのように起こるのかを見ておこう。
磁場がなければジーンズ質量より大きな回転雲は重力収縮を起こす。軸対称2次元のシミュレーションでこれを数値計算するには、たとえば角運動量の数値的な輸送を抑える必要があるなど様々な困難があり、信頼できる結果が得られたのはNorman,
Wilson & Barton (1980)とNarita,
Hayashi & Miyama (1984)の研究によってであった。それらによると、回転しても等温星間雲は回転していないものと同じようにコア形成前に暴走的な収縮を経る。これは遠心力効かないことを示していて、少し考えると矛盾するような気がするが、暴走的な収縮の性質を考えると納得がゆく。つまり、暴走的な収縮では、![]() 程度の空間的に一定の密度
程度の空間的に一定の密度![]() をもつ部分と、その外の密度が中心からの距離の2乗に反比例(
をもつ部分と、その外の密度が中心からの距離の2乗に反比例(![]() )する部分からなるが、時間が経つとともにこの空間的に一定の密度
)する部分からなるが、時間が経つとともにこの空間的に一定の密度![]() をもっていた部分全体が収縮するのではなく、このごく一部分がより高い密度
をもっていた部分全体が収縮するのではなく、このごく一部分がより高い密度![]() をもつ一様な中心部を構成し、残りの大部分は
をもつ一様な中心部を構成し、残りの大部分は![]() の部分になってゆく。こうして無限小の質量が無限大の密度に到達するまでこのプロセスは続く。角運動量も外側の大きな比角運動量を持つ部分から
の部分になってゆく。こうして無限小の質量が無限大の密度に到達するまでこのプロセスは続く。角運動量も外側の大きな比角運動量を持つ部分から![]() の部分に残されてゆき、ごく中心の角運動量無限小の質量が無限大の密度に到達すると考えれば回転している等温雲でも暴走的収縮が起こることは納得がゆく。したがって角運動量の効果が見えるのは第1コアが形成された後ということができる。そこではどのような現象が見られるのであろうか。
の部分に残されてゆき、ごく中心の角運動量無限小の質量が無限大の密度に到達すると考えれば回転している等温雲でも暴走的収縮が起こることは納得がゆく。したがって角運動量の効果が見えるのは第1コアが形成された後ということができる。そこではどのような現象が見られるのであろうか。
6.双極分子流と光学ジェット
星形成過程にある分子で同定される分子雲コアや赤外線源近くでは、双極分子流と呼ばれる対称な2方向に向かう分子の流れが観測される。その流れ出る速度![]() はガスの温度10K程度の音速200m/s比べて非常に大きい。収縮運動である星間雲から星への重力収縮過程でどのようにして正のエネルギーを持ったガスが放出されるのかは非常に興味深い問題である。
はガスの温度10K程度の音速200m/s比べて非常に大きい。収縮運動である星間雲から星への重力収縮過程でどのようにして正のエネルギーを持ったガスが放出されるのかは非常に興味深い問題である。
この加速メカニズムとして、流体力学的加速、中心星の輻射による加速などのモデルが検討されたが、現在では、回転するディスクによってひねられたポロイダル磁場(子午面を走っている成分をポロイダル、それに直交する方向の成分をトロイダルと呼ぶ。たとえば円筒座標では![]() のうち、
のうち、![]() と
と![]() がポロイダル成分で、
がポロイダル成分で、![]() がトロイダル成分にあたる。)がトロイダル成分を形成し、その効果でガスが加速されると考えられている(Uchida
& Shibata 1985, Pudritz & Norman 1986)。
がトロイダル成分にあたる。)がトロイダル成分を形成し、その効果でガスが加速されると考えられている(Uchida
& Shibata 1985, Pudritz & Norman 1986)。
ポロイダル磁場(![]() )はトロイダル電流(
)はトロイダル電流(![]() )から作られるが、磁場によるローレンツ力は
)から作られるが、磁場によるローレンツ力は![]() であるからポロイダル磁場のみが存在する非回転の星間雲の場合、φ方向の力(
であるからポロイダル磁場のみが存在する非回転の星間雲の場合、φ方向の力(![]() )は生じない。ポロイダル電流(
)は生じない。ポロイダル電流(![]() )とトロイダル磁場(
)とトロイダル磁場(![]() )が形成されて初めて
)が形成されて初めて![]() が形成される。こうなって初めて、磁気トルク
が形成される。こうなって初めて、磁気トルク![]() が形成され、磁場はガスのローカルな角運動量を変化させることができる。もちろん、無限遠にトルクを及ぼさなければ、星間雲の持つ全角運動量が変化するわけではなく、磁場によって影響された範囲の角運動量の分布が変えられることになる。
が形成され、磁場はガスのローカルな角運動量を変化させることができる。もちろん、無限遠にトルクを及ぼさなければ、星間雲の持つ全角運動量が変化するわけではなく、磁場によって影響された範囲の角運動量の分布が変えられることになる。
ここではゆっくりと回転する星間磁気雲の進化を軸対称2次元のMHDシミュレーションで調べた例を紹介する(Tomisaka 1998, 2000a,b)。回転の方向は磁場の向きと同じであると仮定している。第1コアが形成する前の進化は、基本的に暴走的収縮であり、2次元的ではあるが自己相似的に収縮が進む。
7.多重格子法
先にも見たように自己重力による過程では自己相似的に収縮が進む。数値シミュレーションでこれを追跡しようとした場合に分解しなければならない構造のスケールは、![]() 程度である。これは中心密度
程度である。これは中心密度![]() の1/2乗に反比例して小さくなるので、距離のスケールは、等温期の最後まで、すなわち
の1/2乗に反比例して小さくなるので、距離のスケールは、等温期の最後まで、すなわち![]() 程度から
程度から![]() 程度までで、
程度までで、![]() 倍に減少するし、第二コアまで追跡しようとしたら、
倍に減少するし、第二コアまで追跡しようとしたら、![]() に達するまでで
に達するまでで![]() 倍も減少してしまう。たとえ2次元軸対称の数値シミュレーションであっても
倍も減少してしまう。たとえ2次元軸対称の数値シミュレーションであっても![]() の空間ダイナミックレンジをもつためには最低でも
の空間ダイナミックレンジをもつためには最低でも![]() の格子点を計算する必要があって、1つの物理量を記憶するだけでも、100GB(ギガバイト)の100G(ギガ
の格子点を計算する必要があって、1つの物理量を記憶するだけでも、100GB(ギガバイト)の100G(ギガ![]() )倍のメモリーを必要とするのでそのまま計算機で計算することはここ当分不可能である。
)倍のメモリーを必要とするのでそのまま計算機で計算することはここ当分不可能である。
そこで高精度の空間分解能が必要な中心部のみに細かな格子点を準備し、それが必要ではない外縁部は荒い格子点で被い計算をすればよいのではないかというアイデアが生まれた。これを何重にも行うことで必要な部分に必要なだけ空間分解能を割り当てることが可能になる(このような考えに基づく計算法をAMR(Adaptive Mesh Refinement)法と呼ぶ)。ここではAMR法の一種である多重格子法(Nested Grid Method)を用いて計算した。
8.双極分子流と角運動量の流出
先にも述べたように、収縮の様子は中心密度が![]() など密度−温度関係が変化する点を境に大きく変わることが予想される。そこで、ここでは図4を直線の組み合わせで近似し、圧力を密度の関数として次のように近似できて、4つの部分からなるポリトロープとして扱った。
など密度−温度関係が変化する点を境に大きく変わることが予想される。そこで、ここでは図4を直線の組み合わせで近似し、圧力を密度の関数として次のように近似できて、4つの部分からなるポリトロープとして扱った。
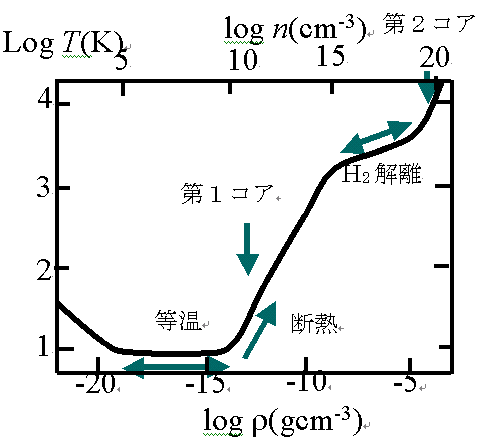
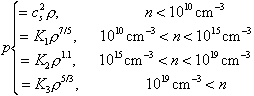 (15)
(15)
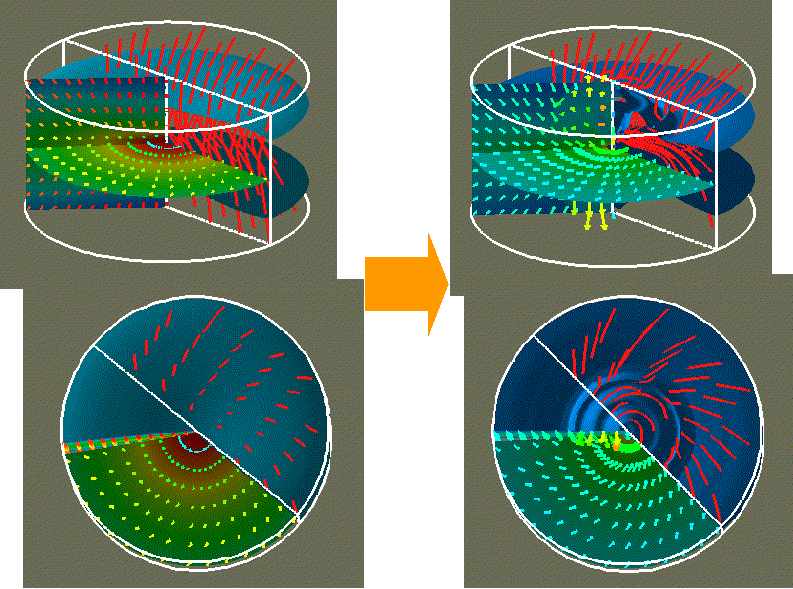
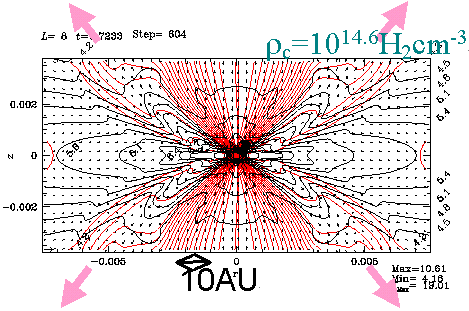
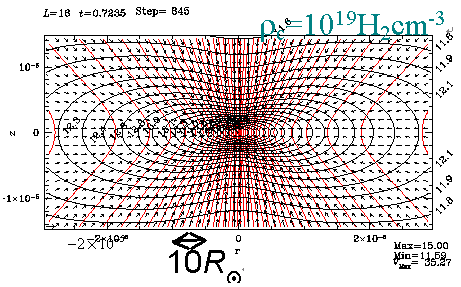
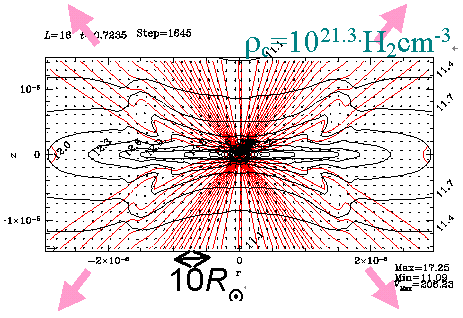
上は横から、下は対称軸付近から見た図で、青色は等密度面、矢印は速度場、赤い線は磁力線を表す。差し渡しは約300AU、左と右の時間差は約1000年である。
ガスが等温である間は前に述べた暴走的収縮が起こっているが、回転している磁気雲の場合もまた同様である。そこでは、磁場のローレンツ力が磁場に垂直方向の収縮を遅くするせいで、磁場に垂直な向きのディスクが形成され、それが中心に向かって収縮している。注意してほしい点は、(1)ディスク内で、ガスは磁場を内向きに引きずる運動をしているが、磁場はほとんど曲げられてなく、(2)ガスは角運動量を持ってはいるが、回転運動は顕著ではなく、収縮運動はほぼ動経方向を向いているという点である。
中心部で、ガスの状態方程式が変化して断熱的になるとどのような構造の変化が起きるのだろうか。速度ベクトルで見られるように、断熱的なってからおよそ1000年後(右図)にはディスクから垂直方向の流れアウトフローが発生する。このとき、ディスク内の構造も同時に変化していて、(1)磁場はガスに引きずられて構造が変化し、砂時計の形に絞られている。(2)ディスク内の回転運動が顕著になっている。これらの要素が相まってアウトフローが発生すると考えることができる。このアウトフローは比較的大きな構造なので分子線観測で見つかる双極分子流に相当すると考えられる。
磁場によって駆動されディスクから発生する磁気遠心力風のモデルはBlandford &
Peyne (1982)によって計算されているが、ここでは彼らのモデルのエッセンスをとりだした説明をしておく。中心星の重力と遠心力の釣り合ったケプラー・ディスクに磁場が貫いた構造を考える。ガスの圧力と自己重力を無視して、定常的にアウトフローが起こっている状況を考える。簡単にするために、磁場はながれによって変形されないと仮定する。この状況では磁場が定常であるためには、ガスは、磁力線に沿って流れ出したとしても角速度を保たなければならない(isorotation)。ガスの角速度は、流れ出す根本の中心星からの距離をrdとすると![]() であるから、遠心力ポテンシャル込みの有効ポテンシャルは、
であるから、遠心力ポテンシャル込みの有効ポテンシャルは、
![]() (16)
(16)
のように書ける。ここで![]() は対称軸からの距離、
は対称軸からの距離、![]() は中心星からの距離をあらわす。磁力線に沿ってガスが流出するとき、この有効ポテンシャルが減少するようになっている磁力線上ではガスは加速され、増加するようになっている磁力線上では加速されないということがわかる。(16)式の有効ポテンシャルを点
は中心星からの距離をあらわす。磁力線に沿ってガスが流出するとき、この有効ポテンシャルが減少するようになっている磁力線上ではガスは加速され、増加するようになっている磁力線上では加速されないということがわかる。(16)式の有効ポテンシャルを点![]() の周りでテイラー展開すると、
の周りでテイラー展開すると、
![]() (17)
(17)
のようになるから、加速と減速の境目は、![]() にあることになる。つまり、
にあることになる。つまり、![]() であるような立った磁力線の場合は加速できず、
であるような立った磁力線の場合は加速できず、![]() のような寝た磁力線の場合は加速することができることがわかる。この条件は、「ディスクと磁力線のなす角が
のような寝た磁力線の場合は加速することができることがわかる。この条件は、「ディスクと磁力線のなす角が![]() より寝ている場合は加速される」と読むこともできる。
より寝ている場合は加速される」と読むこともできる。
ここでは質点の重力の場合を考えて![]() が磁気遠心力加速(磁場によって角運動量を外向きに輸送することによって生じた遠心力で加速するメカニズム)が効果的に働くための条件であることを得たが、ひろがった重力源の分布の場合も基本的には同じで、加速がよく働くためには、磁力線とディスクのなす角が小さいことがエッセンスであることがわかるだろう。
が磁気遠心力加速(磁場によって角運動量を外向きに輸送することによって生じた遠心力で加速するメカニズム)が効果的に働くための条件であることを得たが、ひろがった重力源の分布の場合も基本的には同じで、加速がよく働くためには、磁力線とディスクのなす角が小さいことがエッセンスであることがわかるだろう。
等温ガスの暴走的収縮過程から、中心が断熱的になりそこへ等温のガスが降り積もる降着過程へ移行すると、(1)ディスクの収縮運動による磁場の引き込みが起こり、(2)ディスクのすぐ上部にトロイダル磁場の強い部分が形成されその磁気圧によって圧縮される効果とあいまって、砂時計型の磁力線が形作られる。その結果、暴走的収縮過程ではほとんど直交していた磁場とディスクのなす角は減少し磁気遠心力加速が効果的に起こる条件が設定される。
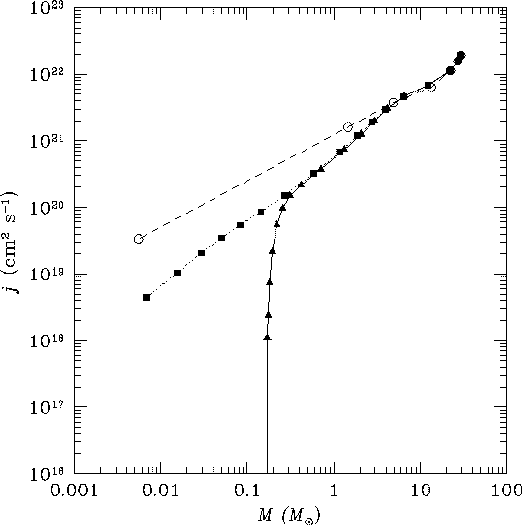
この磁気遠心力加速では加速されるアウトフローガスは磁場から角運動量を得、その根本にあるディスクのガスは磁場によって角運動量を失ってさらに内部に落下する。この過程で、角運動量は生成する星と流出流にどのように配分されるのだろうか。シミュレーションによると、流出するガスの質量の落下するガスに対する割合は10%から20%に達することがわかった。もし、0.1%の角運動量を90%の質量をしめるガスが持って落下して星を形成し、残りの99.9%の角運動量を10%の質量のガスが持って流出したとすれば、形成された星のもつ比角運動量は母体の分子雲コアのそれの〜1/1000にまで減少することになる。これで、「星の角運動量問題」は解決されるのではないか。これを調べるために比角運動量の分布を調べたのが図6である。横軸は中心の密度の高い部分から順に測った質量で、縦軸はその質量の持つ比角運動量である。点線は進化の極初期のもの、破線は暴走的収縮期の最後の時点のもの、そして実線は降着期に入って7000年後の角運動量分布である。大きな質量に対して比角運動量が変化しないのは、角運動量のトータルは保存し変化するのは角運動量の分布だけであるからである。この図だけ見ると、等温の暴走的収縮期にも角運動量の再配分が起こっているように見えるが、これは、もともと角運動量の少ない回転軸付近のガスがいち早く高密度になるからで、角運動量の選択過程であって輸送ではない。それは、比角運動量を横軸にとり、縦軸にその角運動量をもつ質量をとった角運動量スペクトルをとると、その分布が等温の暴走的収縮期には変化しない(全てのガス要素に対してその角運動量が保存していることを示す)ことからわかる。
しかし断熱コアができて以降の降着期においては角運動量スペクトルは変化し、再配分が起こっていることがわかる。そして図6からは、7000年の間に中心に形成される0.2M?の質量では角運動量が![]() まで減少していることがわかる。形成される星の自転角運動量程度までその値が減少することが示されたことになる。
まで減少していることがわかる。形成される星の自転角運動量程度までその値が減少することが示されたことになる。
9 光学ジェット
赤外線源のまわりには光学ジェットと呼ばれるアウトフローが見られる。L1551 IRS5にはすばる望遠鏡によって2本の光学ジェットが、双極分子流の中心部分に見つかっている。この光学ジェットは双極分子流よりも幅が狭いだけでなく、流出速度も速いので、コンパクトな重力ポテンシャルの深い(たとえば星の近くなどの)部分から生じていると考えられている。そのような可能性は、重力収縮してゆく過程でどこで現れるのだろうか。
図3に戻ってみよう。双極分子流は中心で第1コアが形成されるときその周囲の等温ガスが磁気的に加速されたものである。第2収縮から第2コア形成までの進化は、最初の等温収縮から第1コア形成までの進化と似ているので、第2コア周辺で今度は光学ジェットが形成されるのではないかと考えるのはもっともではないかという予想が立つ。
ここに示した計算ではアウトフローの形成の初期しか調べられておらず、この流れが対称軸方向に絞られて(collimation)双極分子流や光学ジェットにまで成長するのは自明ではない。しかし、このディスクとねじられた磁場で形成されるジェットのコリメーションについて調べた工藤ら(2000)のシミュレーションによると、たとえ開いた磁力線にそって流れ出る場合であっても、軸方向に向かうローレンツ力(特に![]() )によって軸方向に向かう加速度が生じ、流れは十分にコリメートされるという結論が得られている。
)によって軸方向に向かう加速度が生じ、流れは十分にコリメートされるという結論が得られている。
10.未解決の問題
先に星形成過程には、「星の角運動量(の余剰)問題」とともに「星の磁束(の余剰)問題」があり、角運動量の方は第1コア形成にアウトフローで角運動量を選択的に捨て去ることで解決する可能性について述べた。磁束の方は、第1コア形成後にコア内部で双極的分散およびジュール散逸によって磁束が失われると考えられている。しかし、第2コア形成時に光学ジェットを形成するためには適当な量の角運動量と磁束がその時点に残っていることが必要である。どれだけの磁束と角運動量が第1コア内部に残るのかを知ることはその後の星の物理量を決める上で決定的に重要である。それには、完全MHDではなく、双極性分散やジュール散逸などの現象をとりいれたさらに精密な計算が必要になる。
また、図6では第1コアの比角運動量は前主系列星のそれに近い値まで減少していたが、これはもっとも効果的に角運動量が輸送された場合の話であることに注意しておきたい。連星系が第1コアの分裂の結果生じたものであるとし、単一星ではなく連星系を作るという立場からすると角運動量は連星系のそれ程度になっているはずで、それらがどのように決まっているのかを考えることも必要であろう。
引用文献
Bonnor 1956: MNRAS 116,351
Ebert 1955: Z. Ap 37,222
Mouschovias, T.Ch., Paleologou, E.V., & Fiedler, R.A. 1985, ApJ, 291, 772
Nakano, T. 1979, PASJ, 31, 697
Narita, S. Hayashi, C., Miyama, S.M. 1984, PTP, 72, 1118
Norman, M.L., Wilson, J.R., & Barton, T.R. 1980 Apj, 239, 968
Pudritz, R.E., & Norman, C.A. 1986, ApJ, 301,571
Tohline, E. 1982, Fundamentals of Cosmic Physics, 8, 1
Tomisaka, K. 1998, ApJ, 502, L163
---------. 2000a, ApJ, 528, L41
---------. 2000b, in Proceedings of IAU Symposium #200 in press
Tomisaka, K., Ikeuchi, S., & Nakamura, T. 1988, ApJ, 335, 239
Uchida, Y., & Shibata, K. 1985, PASJ, 37, 515
流体力学の運動方程式
![]() (A1)に、位置ベクトルrを掛けて体積積分すると、ビリアル関係式が得られる。星間雲の構造が球対称(半径R)で、密度は一様、一定の温度を保っていると仮定する。磁場に関しては適当な形状を仮定すると、
(A1)に、位置ベクトルrを掛けて体積積分すると、ビリアル関係式が得られる。星間雲の構造が球対称(半径R)で、密度は一様、一定の温度を保っていると仮定する。磁場に関しては適当な形状を仮定すると、
![]() (A2)
(A2)
となる。ここで、![]() は球の慣性モーメント、
は球の慣性モーメント、![]() は熱運動と星間雲内部の運動による運動エネルギーに相当する項(ここで
は熱運動と星間雲内部の運動による運動エネルギーに相当する項(ここで![]() は星間雲内部の無秩序運動も込みにした空間平均した「圧力」で、
は星間雲内部の無秩序運動も込みにした空間平均した「圧力」で、![]() は星間雲の体積)、さらに、
は星間雲の体積)、さらに、![]() は表面の圧力
は表面の圧力![]() に起因する項である。磁場に起因するものは3つの項からなるが、星間雲を貫く磁束
に起因する項である。磁場に起因するものは3つの項からなるが、星間雲を貫く磁束![]() (
(![]() と
と![]() はそれぞれ)を用いて書くと
はそれぞれ)を用いて書くと
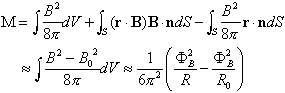
(A4)
のように書き下すことができる。最後に、自己重力に関する項は1のオーダーの係数aを使って![]() の様に書ける。一様密度の場合はa=1をとる。
の様に書ける。一様密度の場合はa=1をとる。