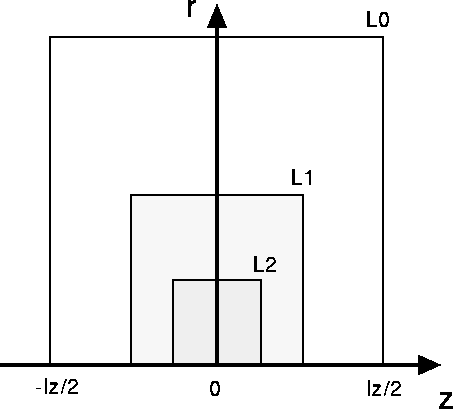
 図1:多重格子法の概念図。L0、L1、L2の三つのレベルからなる多重格子を示す。図はz軸が横軸、動径座標が縦軸であることに注意。実際には15レベルを用いて計算した。
図1:多重格子法の概念図。L0、L1、L2の三つのレベルからなる多重格子を示す。図はz軸が横軸、動径座標が縦軸であることに注意。実際には15レベルを用いて計算した。
1.はじめに
2.自己重力の性質
3.多重格子法と星間雲の収縮
4.まとめ
図の説明
 図1:多重格子法の概念図。L0、L1、L2の三つのレベルからなる多重格子を示す。図はz軸が横軸、動径座標が縦軸であることに注意。実際には15レベルを用いて計算した。
図1:多重格子法の概念図。L0、L1、L2の三つのレベルからなる多重格子を示す。図はz軸が横軸、動径座標が縦軸であることに注意。実際には15レベルを用いて計算した。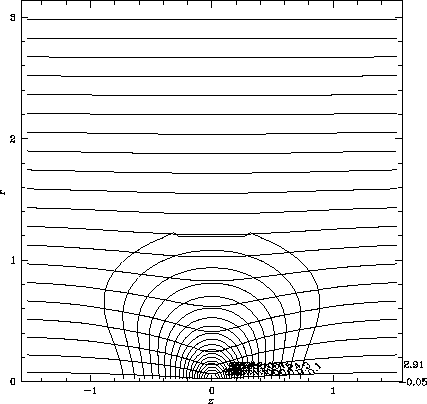 (a)釣合の状態にある初期状態。L2での密度の等高線(ほぼ円形)と磁力線(z方向に走っている)を示す。横軸のz軸が対称軸。
(a)釣合の状態にある初期状態。L2での密度の等高線(ほぼ円形)と磁力線(z方向に走っている)を示す。横軸のz軸が対称軸。
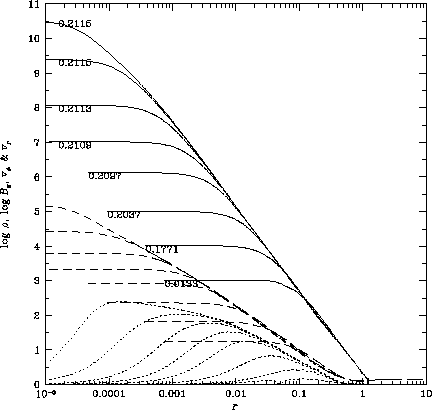 (b)赤道面上(z=0)の密度(実線)、磁束密度(破線)、収縮速度(点線)の分布。数字は収縮開始からの時間tを表しており、磁束密度、収縮速度ともより上側の線が時間が経過した状態に対応している。密度と磁束密度は対数目盛、速度は内向きの値をそのまま示している。横軸が距離の対数目盛である点に注意。
(b)赤道面上(z=0)の密度(実線)、磁束密度(破線)、収縮速度(点線)の分布。数字は収縮開始からの時間tを表しており、磁束密度、収縮速度ともより上側の線が時間が経過した状態に対応している。密度と磁束密度は対数目盛、速度は内向きの値をそのまま示している。横軸が距離の対数目盛である点に注意。
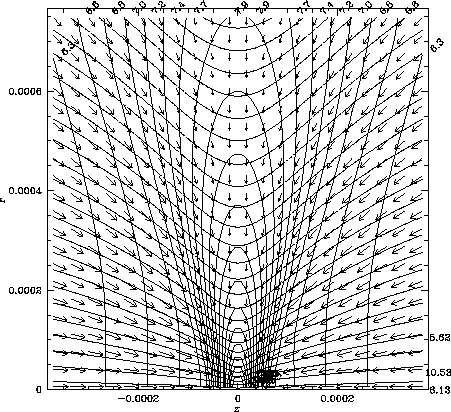 (c)中心密度が表面の1010倍に達した最終状態をL14格子でみたもの。図(a)と212=4000倍だけ縮尺が異なることに注意。密度等高線(主に縦方向に走っている)の込んでいる部分に等温斜め衝撃波が生じており、z方向からきた流れはここで減速、圧縮される。衝撃波面に挟まれて高密度のディスクが生じている。磁力線(主に横方向に走っている)がディスクの動径方向への収縮に引きずられていることがわかる。
(c)中心密度が表面の1010倍に達した最終状態をL14格子でみたもの。図(a)と212=4000倍だけ縮尺が異なることに注意。密度等高線(主に縦方向に走っている)の込んでいる部分に等温斜め衝撃波が生じており、z方向からきた流れはここで減速、圧縮される。衝撃波面に挟まれて高密度のディスクが生じている。磁力線(主に横方向に走っている)がディスクの動径方向への収縮に引きずられていることがわかる。