１．基礎編
１．１ 天体からの光
1.1
連続スペクトルと輝線スペクトル
プリズム分光器（写真\
ref{pic:prizm}）で光を波長別に分解する（分光）と、太陽光のように赤色（およそ波長
=600nm）から紫色（波長=400nm）にわたって、すべての色の光を含んでいる。それに対して、街路の照明に使われている水銀灯やトンネルの照明に使われているナトリウム灯などを分光すると、輝線と呼ばれる特定の波長の光だけを含んでおり事が分かる。
前者のように様々な色の光を連続的に含んでいるものを連続スペクトルと呼び、後者のように特定の波長の光だけを含む輝線スペクトルと呼ぶ。輝線スペクトルで、どの波長の光を出すかということは、光を出している元素の種類およびそのイオン化状態などでおのおの異なっている。
太陽からの輻射は連続スペクトルを示すが、これは黒体輻射と呼ばれる一般に「熱いもの」からの輻射である。この「熱いもの」からの輻射は次のような特徴を持っている。
（１）物体の温度が上がるにつれて、もっとも沢山のエネルギーを放射する波長が短くなる。その結果、温度の上昇とともに、出てくる輻射の色は赤から青い方に変化する。
（２）物体の温度が上がるにつれて、どの波長でも、波長あたりに出すエネルギーは
増大する。その結果、輻射の強度が増す。
1.2
黒体輻射
この黒体輻射の性質をどのように理解すべきかは２０世紀初頭の大きな問題であった。プランクによって、エネルギー量子の考え（やりとりできるエネルギーに基本的な単位が存在するという全く新たな考え）が導入されて初めて、それに基づいて得られた黒体輻射のエネルギー分布は、測定されたものを説明することができた
(1900)。プランクによって得られた輻射法則を、もう少し詳しく見てみよう。絶対温度Ｔ(K：ケルビンと読み絶対温度の単位。摂氏０度は約273Ｋにあたる)の「熱いもの」の表面からでてくる輻射は、その単位時間当たりのエネルギー放出率はその表面積に比例するが、(もし等方に放射されていれば)単位面積あたり、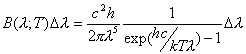から
の波長の光で
のエネルギーが放出される（プランクの式）。ここで、ｃ、ｈ、ｋはそれぞれ光速、プランク定数、ボルツマン定数である。
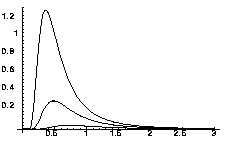
温度Ｔを変えて、この式
をグラフに書くと図のようになる。温度を上げるにつれて、強度が最大になる波長
が短くなっていることが分かる。このは温度Ｔと
のように反比例する。これをウイーンの法則
(1893)と呼ぶ。また、単位時間に単位面積から放射される光のエネルギーＬは温度Ｔが高いほど大きくなり、プランクの式を
で積分すると、
となる（シュテファン-ボルツマンの法則1879,1884）。
1.3
線スペクトルとドップラー効果
先に見たように、太陽からくる光が、プランクの黒体輻射の式で表される連続スペクトルを示したのに対して、水銀灯やナトリウム灯からの光や「炎色反応」によって物質を熱したときに出る光は元素によって決まった色の線スペクトルを持っていた。
光を含む電磁波が、電場と磁場の変化によって伝わる「波」であり、電子など荷電粒子が加速度運動をする場合に電磁波が放出されることは、マックスウェルによって
19世紀後半に理論的に予言された。そうであれば、荷電粒子（電子など電荷を持った粒子）に電磁波が当たると
（電荷×電場）の振動する力が働き、荷電粒子は加速度運動をする（水面の波によって浮かんだ落ち葉が浮き沈ように）。[この原理によって電磁波を電子の流れである電流に変えるのがアンテナの役目である。]この電磁波の存在は、ヘルツ（1988）による実験によってその後に確かめられた。
それでは線スペクトルはどのようなメカニズムで放出されるのであろうか。
巨視的な物体と同じように、もし、正の電荷を持つ原子核の周りをまわる電子（負の電荷をもつ）が回転に伴って電磁波（光）を出すのだとすると、電磁波として運び去られるエネルギーの分だけ、電子は運動エネルギーを失い、瞬く間に中心の原子核に衝突し、吸収されてしまうだろう。実際にはそういうことはないし、さらに、このプロセスが実際に働いたとしても、軌道が縮まるのにともなってでてくると予想される電磁波の振動数は増加するので、電磁波は連続スペクトルを示すことになるだろう。
1.3.1
量子化
この問題を解決するには、微視的な物体に働く法則が巨視的な物体に対するものと少し異なっていることに気がつく必要があった。微視的なスケールでは、ものは波としての性質を持つことが知られている（ド・ブローイ）。たとえば電子顕微鏡では、電子というものが小さなスケールでは光と同じ波としての性質をもつことを小さいスケールの構造をみるのに利用している。物質（たとえば電子）の運動量を
とすると、この波は
の波長をもつと考えると、波の干渉などの現象をうまく説明できた。
はプランク定数を表す。
この原子核の周りをまわる電子のド・ブローイ波が、定在波となる条件として、軌道の円周の長さ
(
)が波長(
)の整数倍になる軌道のみが存在すると考えると（これはあくまでボーアの立てた作業仮説であって結果が現象を説明して始めて認められるものであるが）、半径
と電子の回転速度
の間には次のような関係が成り立たなければならない
。
ところが、円軌道の半径とその軌道を運動する電子の速度の間には、（円運動をするために、電子（電荷
）が原子核（電荷
）に引きつけられている電気的な力と遠心力が釣り合っていなければならない）
の関係があるので、
のようなとびとびの半径の軌道（それぞれエネルギーが異なる）のみが許されることになる。ここで
、
と
はそれぞれ、真空の誘電率、原子番号、電子（陽子）の電荷をあらわす。そして、許される異なる軌道へ電子が移った場合に、全エネルギーの差が電磁波として放出されるとすると、放出される光の線スペクトルの波長がよく説明される。これを最初に提唱したのはニールス・ボーアであった
まとめると、古典力学に従う惑星の運動のような場合では、軌道半径は連続的に変化しうるが、微視的なスケールでは、ある軌道をとった場合のみ、ある離散的なエネルギーの状態のみが許されるという違いがある。
このように、線スペクトルは、元素やイオン化状態によって決まった波長の輝線スペクトルを放射することがわかった。したがって、その輝線スペクトルがどんな元素のどのようなイオンによって放射させているものであるかがわかれば、地上の実験によって、その光の波長を決めることができる。
1.3.2
ドップラー効果
波の発生源（音ならば音源）と観測者が互いに近づいているときは、波の振動数は大きくなり（音なら高くなり）、遠ざかっているときは、反対に振動数は小さくなる
(音なら低くなる）。これを、ドップラー効果という。そのわけは、発生源で
1秒間に
回振動したとする（振動数が
Hz）と、止まっている観測者には、同じく1秒間に回振動の山または谷が到着する（振動数がHz）。ところが、速度
(m/秒)で遠ざかっている観測者は、1秒間に
(m)だけ発生源から離れるので、この(m)の距離に含まれる山または谷の分だけ、つまり
だけ、山や谷を負い越すために、伝わる振動の回数が減少する。波の伝わる速度を
(m/秒)とすると、波長と振動数の間には、
という関係があるので、
だけ振動数が減少する。したがって、観測される振動数は
となる。同じようにして近づいているときには
となる。
この関係を波長に直せば、遠ざかる速度を
という関係があることが分かる。（池の波でわかるようにあくまで波長に直した場合こうなるのであって、長さ自身が変化するわけではない。）
光の場合は正確に計算するためには特殊相対論を使わなければならないが、速さが高速に比べて十分ゆっくりとしている場合には（
）、この関係が成り立つ。したがって、天体から出た元々波長
(m)で観測されたとしたら、この天体は地球から
の速度で遠ざかっていることがわかる。
天文学では、地球
(太陽)から遠ざかったり近づいたりする運動は、このようにして輝線スペクトル（吸収スペクトル）の波長が、実験室で測定されたものと異なっていることを利用して測定している。
1.5 見かけの明るさと光度
太陽からは地球上に降り注いでいる光のエネルギーはどの程度なのだろうか。地球上で太陽方向に向けた
の面積の板が１分あたり受け取る輻射エネルギー流束は、
である。これから、太陽が単位時間に放射している光のエネルギーは
のように求められる。このように恒星が単位時間に放射している光のエネルギーを光度と呼ぶ。
星からの光の輻射エネルギー流束Ｓは、星までの距離をＲとすると
であるから、距離に依存する見かけの量である事が分かる。天文学では輻射エネルギー流束はその常用対数をとった等級という量で表すことが多い。
エネルギー流束が１００倍大きい（小さい）星は５等級小さい（大きい）ことになる。マイナスがついているのは、等級の小さい星が明るい星であるという歴史的理由によっている。
これから、同じ光度を持つ星の場合でも距離によって見かけの明るさは異なることになる。距離が１０倍遠い星の見かけの明るさは５等級暗い（大きい）ことになる。このように天体の見かけの明るさはその天体までの距離によるので、絶対的な明るさ（光度）を表すために、天体を１０パーセク
の距離においたとしたときの等級を絶対等級Ｍと呼び、
光度に相当する量として用いる事ができる。
ここまでは区別していないが、どのような色で見たときの等級かという区別をする場合は
、
、
、のように使う。ここでU、Ｂ、Ｖはそれぞれ紫外線（中心波長365nm）、青（440nm）、実視（人間の目の感度に近い548nm）の光を表す。