2.5
天体の年齢の測定
前節では天体までの距離を測定する方法についてみてきた。これを用いて人類は太陽系から出発して宇宙規模の天体までの大きさを知ることができるようになった。しかしこれだけでは不十分である。宇宙における時間のながれ、過去から現在までになにが起こってきたかを知らなければ宇宙を理解したことにはならない。そのために必要な年齢の測定法について見てみよう。
2.6 放射性同位元素を用いた年代測定法
天体の年齢を測定するには、直接その構成物質が資料として得られる場合には、放射性同位元素を用いた年代測定法が用いられる。その原理を簡単に説明しよう。たとえば炭素元素は、中性子の数の異なる同位体が存在する。自然界には
99%の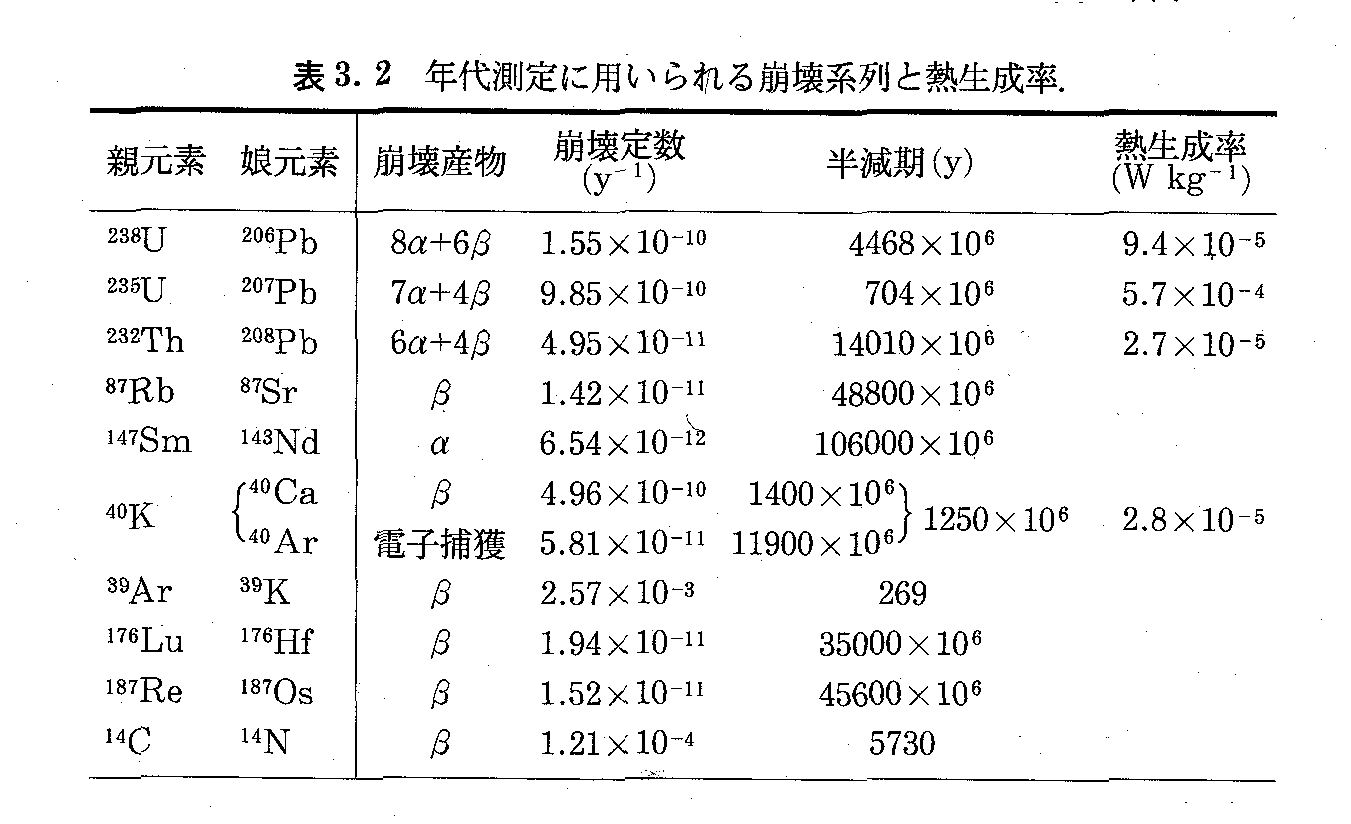
例 ![]() を用いた植物の年代測定。
を用いた植物の年代測定。
大気中の![]() は宇宙線の照射によって生じた中性子と核反応して
は宇宙線の照射によって生じた中性子と核反応して![]() となる。この過程によって、大気中には、ほぼ一定の
となる。この過程によって、大気中には、ほぼ一定の![]() が存在している。生物は体内に
が存在している。生物は体内に![]() も取り込んでいるが、生物が死ぬと新たな取り込みは起こらず、取り込まれていた
も取り込んでいるが、生物が死ぬと新たな取り込みは起こらず、取り込まれていた![]() が
が
![]()
を使って生物が死んでからの時間
tを決めることができる。
岩石の年齢は
K-Ar、Rb-Sr、U-Pbなどのいくつかの方法で調べられる。ここではK-Ar法を簡単に紹介する。 ![]() 半減期
半減期
![]() 半減期
半減期
このような方法で解析を行うと、地球上の岩石のもっとも古いものはおよそ
40億年の年齢を持っていることが分かる。太陽系の年齢(ガスの原始太陽系星雲から固体の天体が形成されたのを太陽系生成の時期だと考えると)は、太陽系と同年代だと考えられる隕石を放射性同位元素を用いた年代測定して約
45億年と見積もられている。
2.7 恒星の年代測定
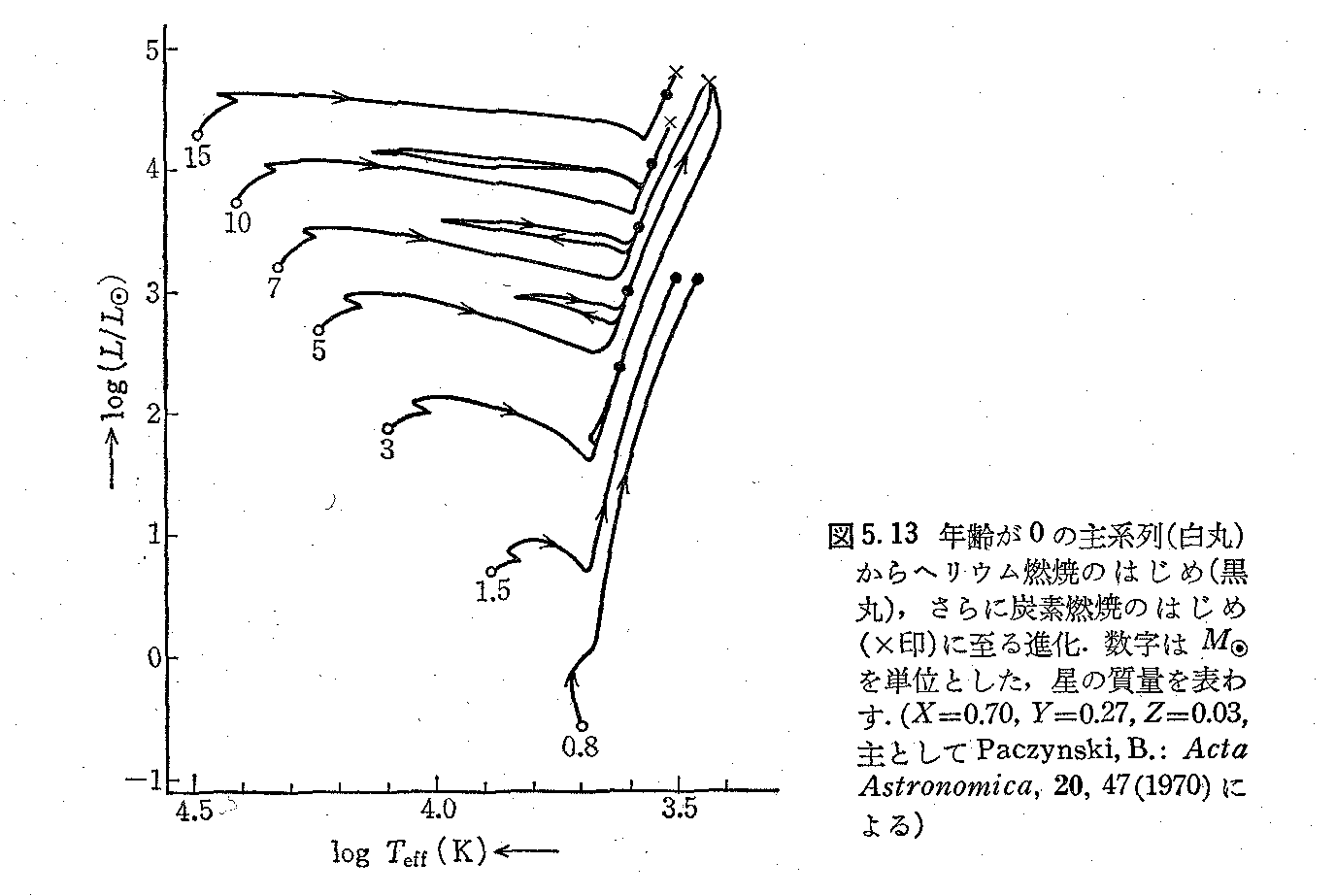

単一星の年齢の決定は、距離が正確にわかっている場合の他は、むつかしいが、球状星団などのように同時に多数の星が生まれたことが分かっているような場合は、星団のHR図を同年代線(アイソクローン)と重ね合わせることによって決定することができる。そのためには、恒星がHR図の上でどのように進化するかを決めることが必要である。大型計算機が科学技術計算に利用できるようになった
1960年代から多くの恒星進化の計算が行われた。その結果、次のようなことがわかった。主系列星の段階a-cでは恒星の中心核で水素がヘリウムに核融合する反応が続く。この時期が恒星の寿命の大半を占め、太陽と同程度の質量の星では約100億年、その5倍のもので5千万年続く。HR図上での位置は星の質量に依存し重い星ほど高温で光度が大きくなる。その後中心部にヘリウムがたまり、星は主系列を離れる。その後、中心部でヘリウムが炭素などの重い元素に核融合する反応が進行する(図の丸印)。質量の重い星はさらに炭素が酸素、ネオンをへて、シリコンへ融合する反応をおこす(図のX印)。詳しい進化の様子は表のようになる。
さて、星が主系列星である期間は、質量が大きな星(HR図で左上にある)ほど短いので、同時に生まれた星団のHR図を考えると、時間とともに左上にある星から主系列を離れて行く。主系列星として生まれた時刻を0として、
3千万年、6千600万年、1億年、42.5億年たった後のHR図を示した。主系列星が高温高光度の左上の領域までのびている方が若く、右下で巨星分枝へ折れ曲がっているほど年齢を経ていることが分かる。このような方法で、ヒッパルコス衛星による年周視差の観測をもとに決めなおした重元素のすくない主系列星の光度をもとにして、銀河系で最も年老いた星団である「球状星団」の年齢を求めるとM5、M13、M92などの球状星団の年齢として110億年から130億年という値が得られている。球状星団、そして我々の銀河は100億年以上の年齢を持っていることが分かる (Reid 1997より)。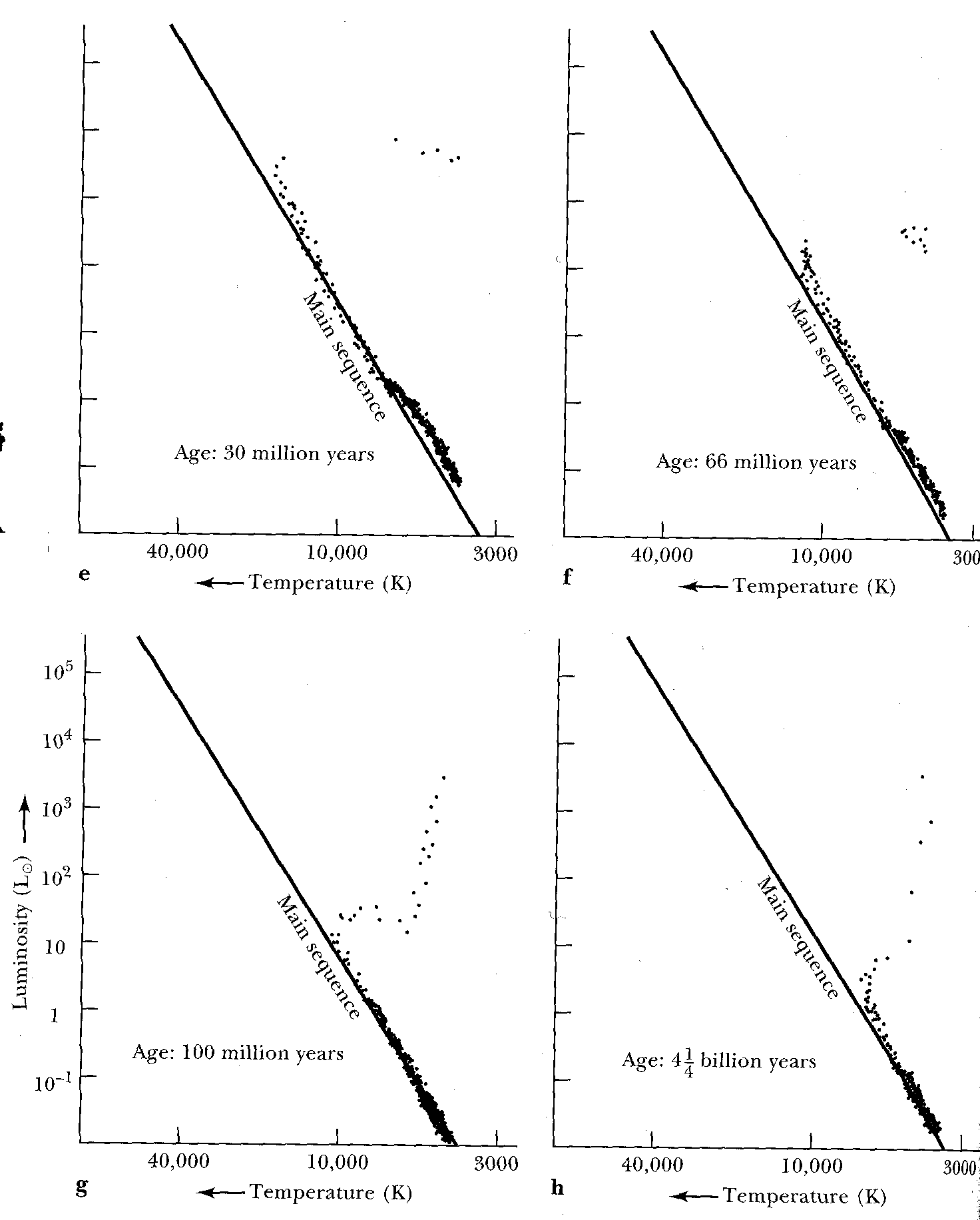
2.8 宇宙の年代
宇宙全体がビッグバンの後どれだけ経過しているかは、現在の宇宙の密度がいくらであるかと、現在のハッブル定数の大きさによっている。問題を簡単にするために、宇宙の密度が大変少なく、したがって重力によって宇宙膨張が減速されない場合を考えよう。そうすると宇宙の曲率半径は
![]()
にしたがって膨張する。右辺の比例係数が![]() に等しいことは、この式をtで微分した式
に等しいことは、この式をtで微分した式![]() がハッブルの法則を意味していることから明らかであろう。現在の時刻
がハッブルの法則を意味していることから明らかであろう。現在の時刻![]() は
は![]() (宇宙半径が現在の値に等しい)として
(宇宙半径が現在の値に等しい)として![]() と求められる。この宇宙膨張が減速されない場合の現在までの時間
と求められる。この宇宙膨張が減速されない場合の現在までの時間![]() は宇宙の年齢の上限を与える。
は宇宙の年齢の上限を与える。![]() であるから
であるから![]() と求められる。後で述べるように、宇宙の密度が臨界密度
と求められる。後で述べるように、宇宙の密度が臨界密度![]() の時には、
の時には、![]() となる(
となる(