まず、天体の距離をどのようにして測定するのかを考えてみよう。地球上の距離の測定では、見通せる距離の場合はレーザー光を発射して反射して戻ってくる間での時間tを測定し、これに光の速度cをかけた２分の１で求められる。現在では同じような方法で月までの距離を正確に決めることができている。

さらに遠い天体の場合は三角測量（既知の距離だけ離れている２点からの見込む角の差によってその距離を知る）によって距離を知る。図のように地球が太陽の周囲を公転するすることによって恒星の見える方向が季節によって変化する（年周視差という）。方向の差を２θとすると、恒星までの距離dは

で与えられる。ここでθ=1”となる距離を1パーセクと呼び、1pcと書く。

問題：θが小さいときtanθ≒θ（ラジアン単位）であることを示せ。証明してもよいし、表を作って比べてもよい。なおθが秒単位であるとするとこの公式tanθ≒θはどのように書き換えられるか。

問題：太陽と地球との平均距離である1天文単位はである。これから1pcがであることを示せ。

　この問題からもわかるように、1pcは約3光年である。この方法でどの程度の距離までの恒星の距離が測れるかは、視差したがって恒星の位置がどの程度の精度で測定できるかによっている。現在地上の観測ではそれは0.”01程度なので、年周視差の方法によって到達できる距離はおおよそ100pc≒300光年にすぎない。

　星団の距離は、ＨＲ図を作成することによって測定できる。星間吸収による恒星からの光の色の変化（赤化）が無視できる場合、その星団を構成する星の色指数と見かけの等級から作ったＨＲ図を、距離のわかった近距離の恒星の色指数と絶対等級の関係HR図から、主系列を合わせることによって、見かけの等級と絶対等級の間の関係

ＨＲ図を用いて主系列星をあわせる方法は、主系列の大多数が低光度であるため、我々の銀河系内の球状星団などの距離決定には利用できるが、より遠方の天体にこれを適用することはできない。さらに遠方の天体に対しては、変光星の周期光度関係を用いて距離が決定されている。これに使われる変光星は、セフォイド型変光星およびRR Lyr型変光星という星の半径が変化することによって明るさの変化する脈動型変光星と呼ばれる一群の星である。

1912年H.リービットは、我々から最も近い銀河であるマゼラン銀河内にあるこの変光星で、変光の周期と光度の間に正の相関があることを見いだした。測られたのは見かけの明るさと変光周期の関係だが、マゼラン銀河内の変光星を使うことによって、これらは同じ距離にあるのだから、マゼラン銀河までの距離はわからなくとも光度と周期の間の相関があることを示すことができた。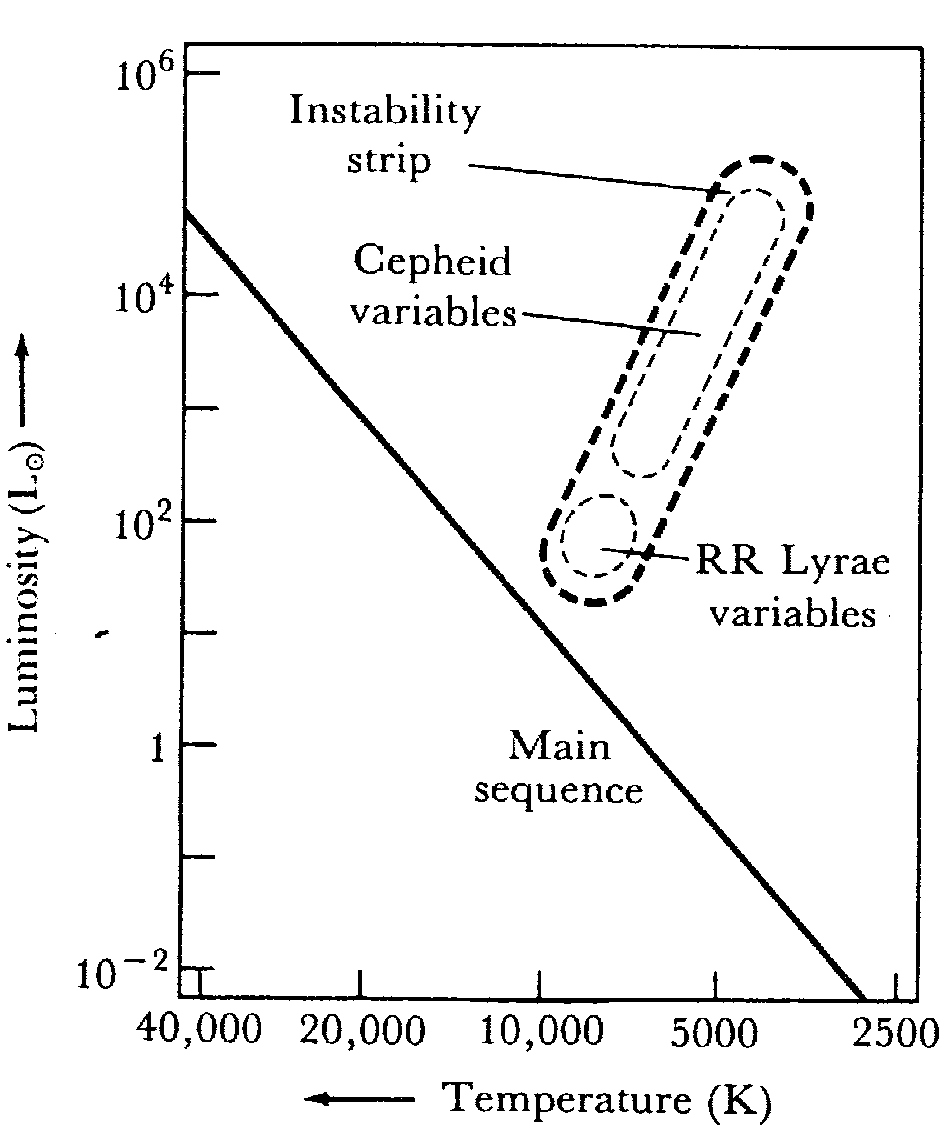

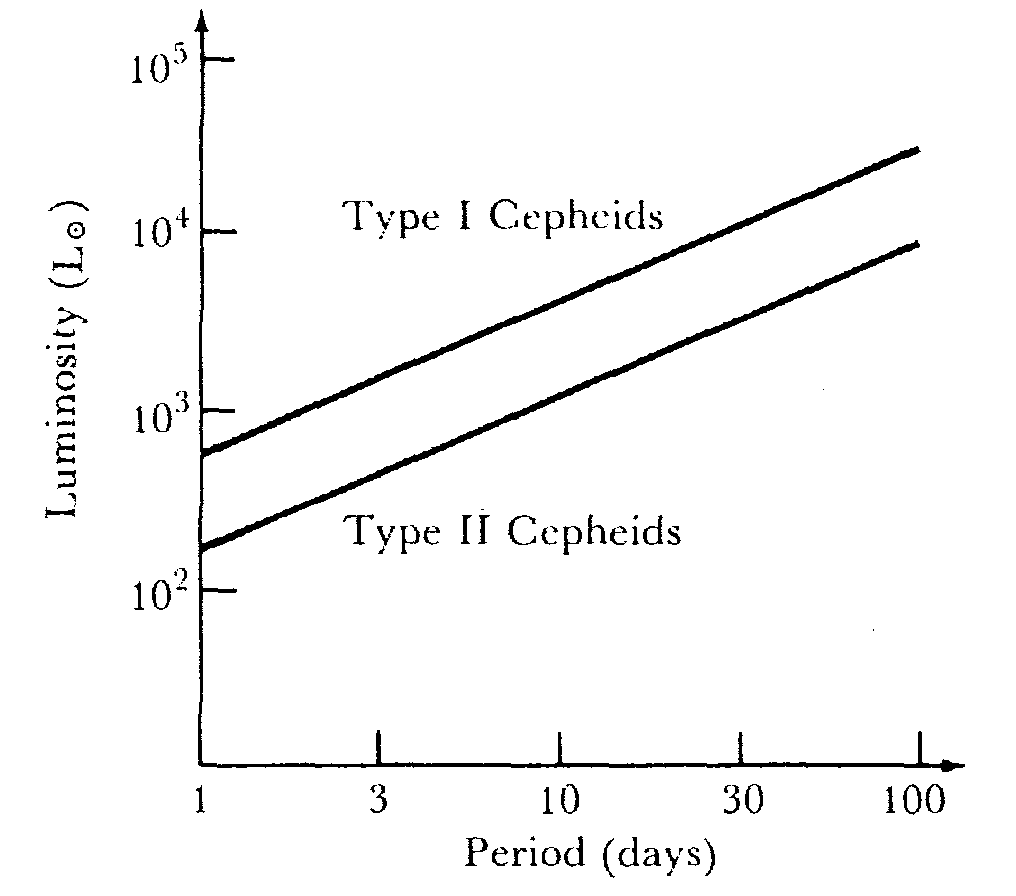
これらの変光星はＨＲ図で不安定帯と呼ばれる特定の場所に位置する星で重要な性質として変光の周期と光度（絶対的な明るさ）の間に正の相関があることである。星団に属していて距離のわかっているこれらの変光星の周期と光度の関係を調べると、１、２日の周期で変光するセフォイドの平均光度は太陽の約１００倍程度であるのに対して、１００日程度の周期で変光するものは太陽の１万倍の光度を持つ。

これからも明らかなように、セファイド型変光星は主系列星に比べて光度（絶対的な明るさ）が大きくそのためにＨＲ図の主系列星の重ね合わせで到達できるよりもさらに遠くの天体の距離を決めることができる。

この関係を使ってハッブルはアンドロメダ銀河（Ｍ３１）までの距離を決定した。１９２４年のことである。現在の観測値を使うとそれはおよそ２５０万光年である。その当時「アンドロメダ星雲」が我々の銀河内の比較的小さな天体であるのか（シャープレイ説）かそれとも我々の銀河と同じような独立した銀河（カーティス説）が対立していた（星雲とは星のように点状にはなくぼーっとしている天体を表した言葉であり、現在では使わない方がよい）。ハッブルは変光星の周期光度関係を使って距離を求めることによって、「アンドロメダ星雲」が我々の銀河と同格の「アンドロメダ銀河」であることを示した。