1.6　ＨＲ図の物理的意味

　

さて、星からの輻射は第一次的には黒体輻射（1.4節）と考えてよい。黒体輻射の性質から、横軸の星の色指数は恒星の表面の温度Ｔと考えてよい。縦方向の違いはなになのであろうか。Ｔが同じ恒星について考えると、プランクの輻射式から、星の表面から単位時間にでる輻射のエネルギー（光度）は星の表面積に比例する。したがって、縦軸方向に上にある恒星の半径は下にあるものより大きいことが分かる。したがって、超巨星、巨星は光度が大きいだけでなく、実際に半径の大きい（巨）星であることが納得できよう。

ステファン・ボルツマンの法則から単位時間あたり半径Ｒの星が放射する全輻射エネルギーは

　　　　　　　　　　　　　

となる。ここではステファン・ボルツマン定数と呼ばれる量である。これから星の半径Ｒは、いずれも観測量である光度Ｌ、温度Ｔを用いて

　　　　　　　　　　　　　

と表されることが分かる。太陽は表面温度5800Ｋの主系列星である。太陽の倍の光度を持つ低温Ｔ=3000Ｋの星であるベテルギウスは、

　　

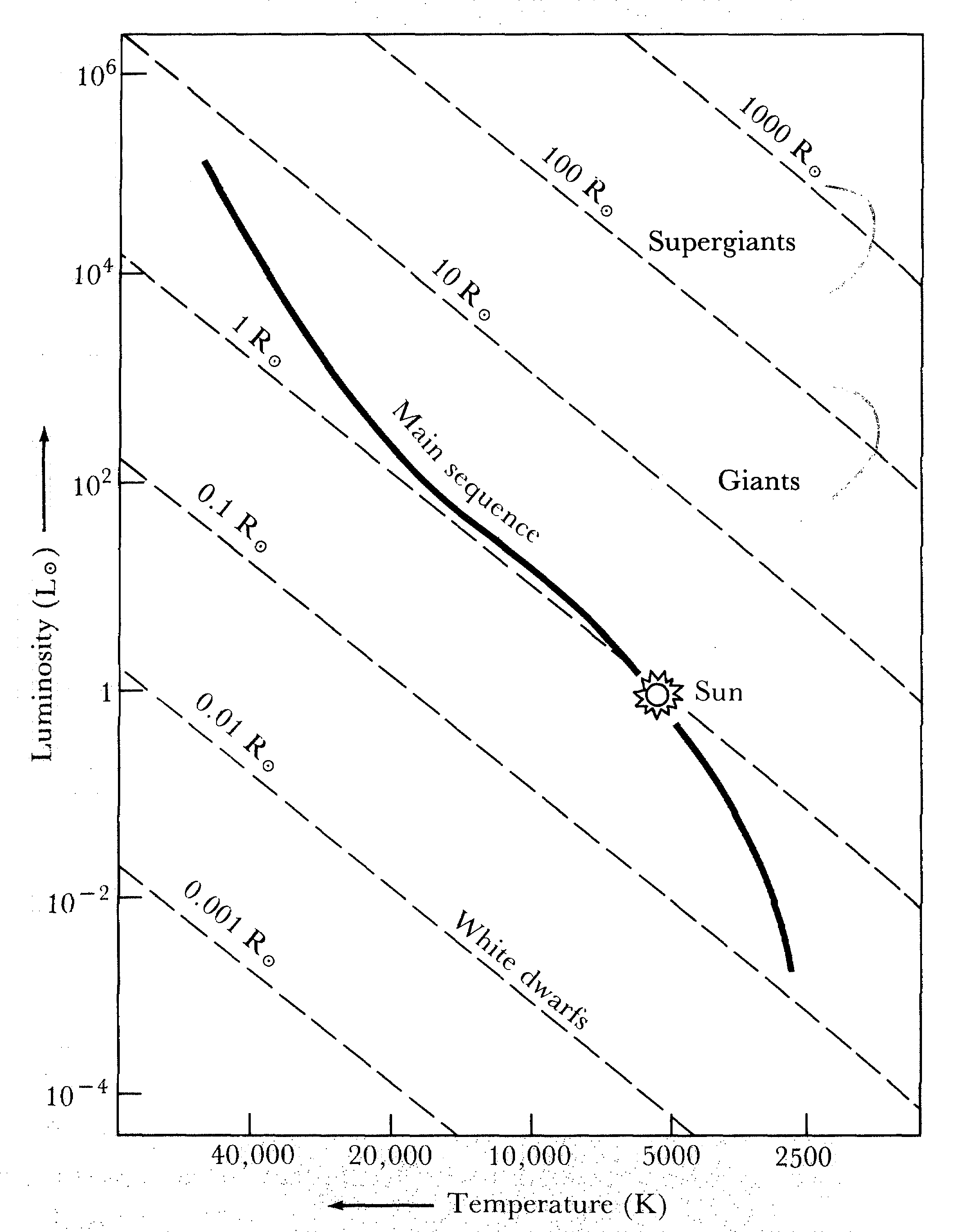
の大きさであることが分かる。恒星の表面温度Ｔと光度Ｌの関係を図に示すと左のようになる。

　

　上の半径一定の線に相当するものを横軸、縦軸実視絶対等級で取ったＨＲ図に書き込むことを考える。ステファン・ボルツマンの法則から、半径、温度の恒星の光度は

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(1)

である。光度から絶対等級に直すには、

　　　　　　　　　　　　　　　　　　　　　　　 (2)

を使えばよいから、絶対等級と恒星の温度、半径の間には

　　　　　　　　　　　　　　　　　　(3)

のような関係があることになる。ここで、などは太陽の半径と温度であり、太陽の全輻射等級が4.75等であることを使った。

　

ここで恒星の色指数は、恒星の色のみによっている。それを決めているのは温度のみであり、恒星の半径にはよらないことに注意すれば、ＨＲ図上に恒星の半径一定の曲線を引くことができる。

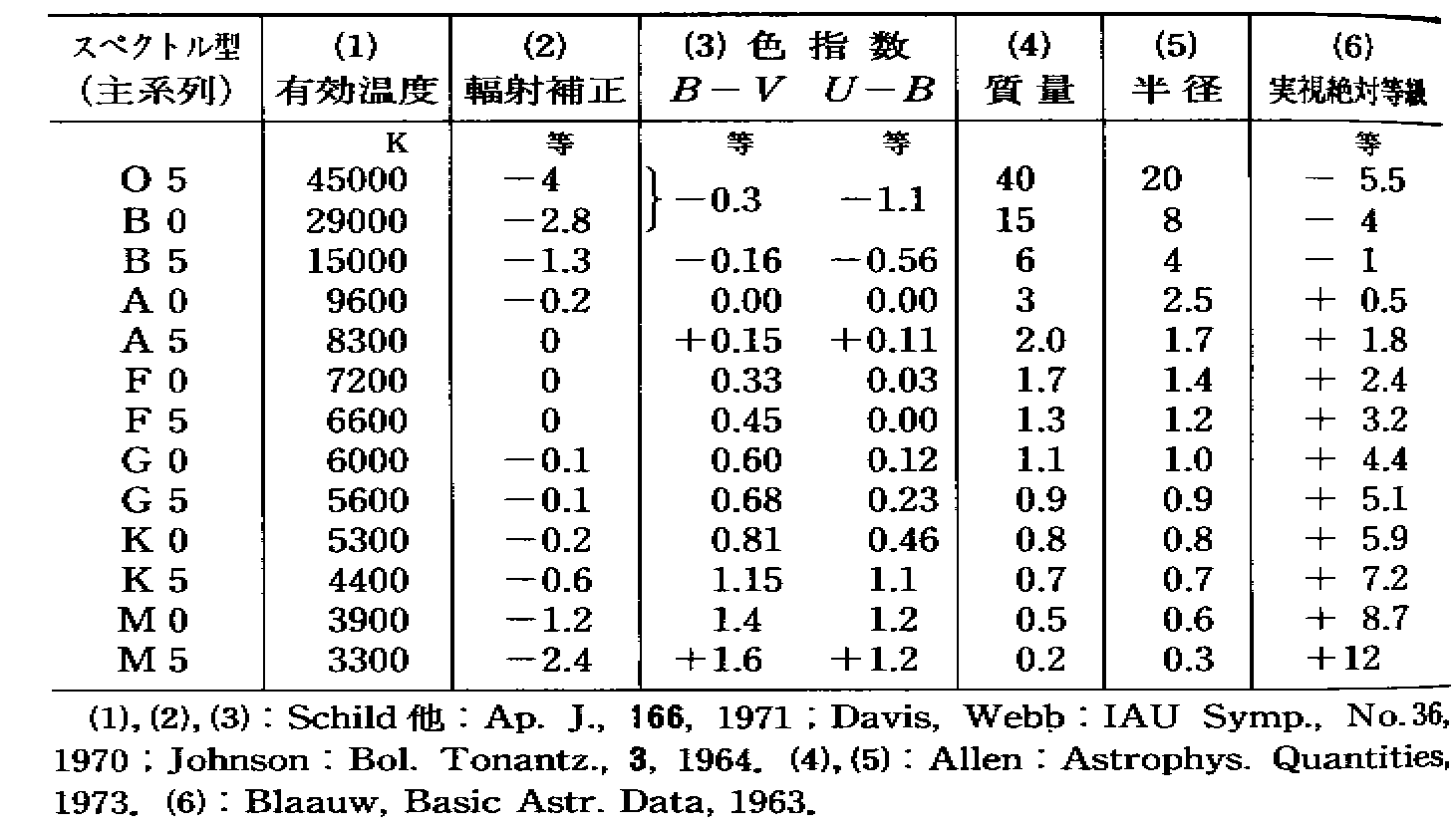
色指数と温度の関係は、定性的には高温のものほどが小さくなり、低温のものほど大きくなるはずであるが、定量的には表　のようになっている。

表　の（１）の温度と（３）の色指数の関係を用いて、ＨＲ図上に、半径が（あ）太陽と同じ恒星、（い）太陽の１０倍、（う）太陽の１００倍の恒星がどのような曲線上に分布するかを示すと以下の図のようになる。ただし太陽の有効温度は5800Ｋであるとした。

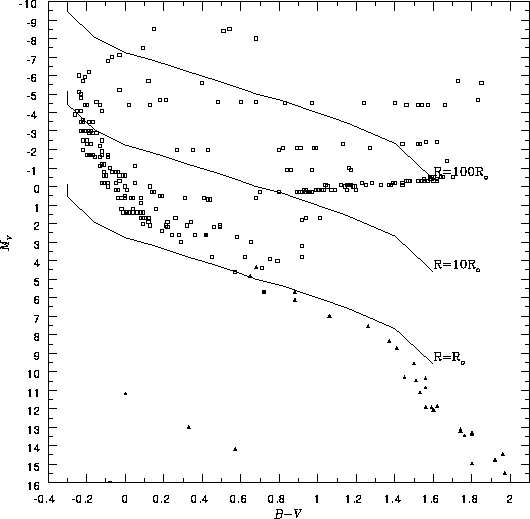
正確に言うと、上の式で求まるのはすべての電磁波で放射されているエネルギーに対応する絶対等級で全輻射絶対等級と呼ばれる量である。したがって、実視絶対等級（Ｖバンドで測定した絶対等級）とは異なっている。その差を輻射補正と呼び、　　　　　　　　　　　　　　という関係がある。この量も表　に示されている。この図は、 (3)式で輻射補正を考慮して、

　　　　　　　　　　　　　　　　(5)

を使用して作成したものである。

　大部分の主系列星の半径は太陽のそれと同程度である。地球軌道の平均半径はおよそであるから、明るい恒星の表に含まれる巨星、超巨星の多くは地球軌道より大きな半径を持っていることになる。