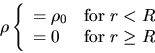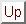


Next: Free-fall Time
Up: The Poisson Equation of
Previous: The Poisson Equation of
Contents
Consider a spherically symmetric density distribution.
Using the Poisson equation, obtain the potential (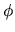 ) and the gravitational acceleration (
) and the gravitational acceleration (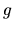 ) for a density distribution shown below.
) for a density distribution shown below.
Hint: The Poisson equation (2.11) for the spherically
symmetric system is
Kohji Tomisaka
2007-07-08