Relation of Einstein's Coefficients to Absorption and Emissivity

Emissivity and absorption coefficients shown in §2.10.1 are related to the Einstein's coefficients in §2.10.2. Net absorption is defined as the absorption minus the induced emission. Energy absorbed in unit volume is expressed as follows: integrating equation (2.123) over the solid angle, the first term of the rhs becomes

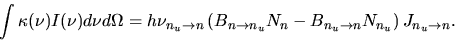$$\int \kappa(\nu)I(\nu)d\nu d\Omega =h\nu_{n_u\rightarrow n} ... ...}N_n-B_{n_u\rightarrow n}N_{n_u}\right) J_{n_u\rightarrow n}.$$ (2.139)

Assuming isotropic radiation field, since

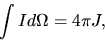$$\int I d\Omega = 4\pi J,$$ (2.140)

the absorption coefficient integrated over the frequency range of one transition is written as

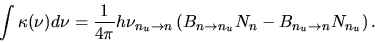$$\int \kappa(\nu)d\nu = \frac{1}{4\pi}h\nu_{n_u\rightarrow n}... ...ft(B_{n\rightarrow n_u}N_n-B_{n_u\rightarrow n}N_{n_u}\right).$$ (2.141)

As for the emission, the second term of equation (2.123) becomes

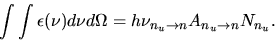$$\int\int\epsilon(\nu)d\nu d\Omega=h\nu_{n_u\rightarrow n}A_{n_u\rightarrow n}N_{n_u}.$$ (2.142)

Thus,

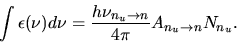$$\int\epsilon(\nu)d\nu=\frac{h\nu_{n_u\rightarrow n}}{4\pi} A_{n_u\rightarrow n}N_{n_u}.$$ (2.143)