Next: Energy Equation Up: Continuity Equation Previous: Continuity Equation Contents
It is useful to describe the equation for momentum
![]() .
Eulerian derivative of momentum density
.
Eulerian derivative of momentum density
![]() is rewritten as
is rewritten as
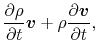 |
|||
| (A.12) |
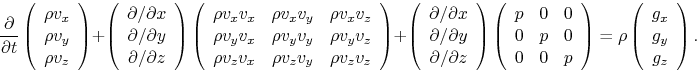 |
(A.13) |
| (A.14) |
If there is no external force, rhs of equation (A.15)
is equal to zero.
If the momentum density
![]() were to obey the continuity equation,
equation (A.15) would be
were to obey the continuity equation,
equation (A.15) would be
Kohji Tomisaka 2009-12-10