Figure B.1:
The change of flux anchored to a surface 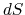 .
One part of the shange comes from the temporal change in magnetic flux density.
The other comes from the change of the boundary of the surface due to
gas motion.
Time variation of the area is given by
.
One part of the shange comes from the temporal change in magnetic flux density.
The other comes from the change of the boundary of the surface due to
gas motion.
Time variation of the area is given by
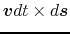 .
.
 |
An important nature of the ideal MHD is derived from equatio (B.4),
that is, the matter and the magnetic field is coupled with each other.
Consider a gas parcel threaded with the magnetic field
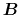 .
The magnetic flux anchored to the gas parcel
.
The magnetic flux anchored to the gas parcel
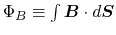 is changes
is changes
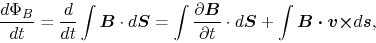 |
(B.5) |
where
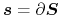 .
The first term of the lhs of the equation comes from a time derivative of the magnetic flux density,
while the last term represents the change of the integral region due to gas motion (see Fig.B.1).
(
.
The first term of the lhs of the equation comes from a time derivative of the magnetic flux density,
while the last term represents the change of the integral region due to gas motion (see Fig.B.1).
(
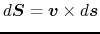 )
Using the Stokes' theorem
)
Using the Stokes' theorem
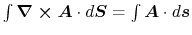 ,
the last term is reduced to
,
the last term is reduced to
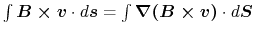 .
Finally, we obtain
.
Finally, we obtain
![\begin{displaymath}
\frac{d \Phi_B}{d t}=\int \left[\frac{\partial \mbox{\boldma...
...${\nabla (v \times B)}$}\right]\cdot d\mbox{\boldmath${S}$}=0,
\end{displaymath}](img1643.png) |
(B.6) |
where we used equation (B.4).
This means that the magnetic flux anchored to a gas parcel does not change in the ideal MHD regime.
Kohji Tomisaka
2009-12-10

![]() .
The magnetic flux anchored to the gas parcel
.
The magnetic flux anchored to the gas parcel
![]() is changes
is changes