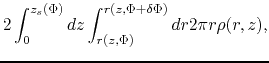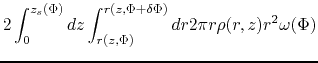In section 4.2, we obtained the maximum mass which is supported
against the self-gravity using the virial analysis.
In this section, we will survey result of more realistic calculation.
Formalism was obtained by Mouschovias (1976a,6), which was extended by
Tomisaka, Ikeuchi, & Nakamura (1988) to include the effect of rotation.
Magnetohydrostatic equlibrium is achived on a balance between the Lorentz
force, gravity, thermal pressure force, and the centrifugal force as
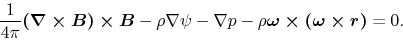 |
(C.13) |
In the axisymmetric case, the poloidal magnetic fields is obtained by
the magnetic flux function, 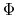 ,
or the
,
or the 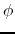 -component of the vector potential as
-component of the vector potential as
Equation (C.13) leads to
with
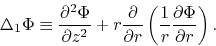 |
(C.18) |
Equation (C.17) indicates 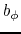 is a function of
is a function of 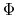 as
as
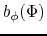 , which is constant along one magnetic field line.
Ferraro's isorotation law demands,
that is, to satisfy the stead-state induction
equation
, which is constant along one magnetic field line.
Ferraro's isorotation law demands,
that is, to satisfy the stead-state induction
equation 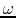 is constant along a magnetic field.
This means
is constant along a magnetic field.
This means 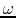 is also constant along one magnetic field line,
is also constant along one magnetic field line,
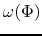 .
From this, the density distribution in one flux tube is written
.
From this, the density distribution in one flux tube is written
![\begin{displaymath}
\rho=\frac{q}{c_s^2}\exp\left[-\left(\psi-\frac{1}{2}r^2\omega^2\right)/c_s^2\right].
\end{displaymath}](img1707.png) |
(C.19) |
This means 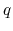 is also constant along one magnetic field line,
is also constant along one magnetic field line, 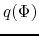 .
Since the forces are expressed by the defrivative of function
.
Since the forces are expressed by the defrivative of function 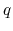
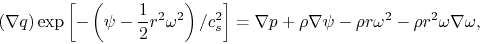 |
(C.20) |
where equation (C.19) is used,
equation (C.15) and (C.16) are rewritten as
Finally, using the fact that 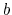 ,
, 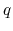 , and
, and 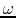 are functions of
are functions of 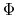 ,
these two equations are reduced to
,
these two equations are reduced to
![\begin{displaymath}
\Delta_1 \Phi=-\frac{d (b_\phi^2/2)}{d \Phi}
-4\pi r^2 \lef...
.../c_s^2\right]+\rho r^2 \omega \frac{d \omega}{d \Phi}\right\}.
\end{displaymath}](img1716.png) |
(C.23) |
Another equation to be coupled is the Poisson equation as
![\begin{displaymath}
\Delta \psi=4\pi G \frac{q}{c_s^2}\exp\left[ -\left(\psi-\frac{1}{2}r^2\omega^2\right)/c_s^2\right].
\end{displaymath}](img1717.png) |
(C.24) |
The source terms of equations (C.23) and (C.24) are given by determining
the mass
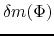 and the angular momentum
and the angular momentum
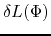 contained in a flux tube
contained in a flux tube 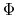 -
-
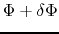 .
Mass and angular momentum distribution of
.
Mass and angular momentum distribution of
is chosen artitrary in nature, where 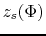 is the the height of the cloud surface where
the magnetic potential is equal to
is the the height of the cloud surface where
the magnetic potential is equal to 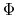 .
For example,
.
For example, 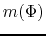 and
and 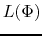 are chosen
as a uniformly rorating uniform-density spherical cloud threaded by uniform magnetic field.
Since
are chosen
as a uniformly rorating uniform-density spherical cloud threaded by uniform magnetic field.
Since
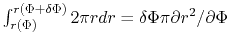
The source terms of PDEs [eqs (C.23) and (C.24)] are given
from equations (C.27) and (C.28).
While the functons 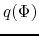 and
and 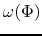 are determined from the solution of these PDEs
after
are determined from the solution of these PDEs
after 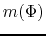 and
and 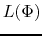 are chosen.
This can be solved by a self-consistent field method.
are chosen.
This can be solved by a self-consistent field method.
Kohji Tomisaka
2009-12-10
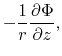
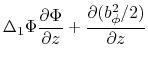
![$\displaystyle -4\pi r^2\left\{\frac{\partial q}{\partial z}\exp\left[ -\left(\p...
...right)/c_s^2\right]+\rho r^2 \omega \frac{\partial \omega}{\partial z}\right\},$](img1712.png)
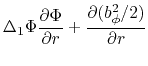
![$\displaystyle -4\pi r^2\left\{\frac{\partial q}{\partial r}\exp\left[ -\left(\p...
...right)/c_s^2\right]+\rho r^2 \omega \frac{\partial \omega}{\partial r}\right\}.$](img1714.png)