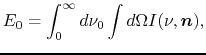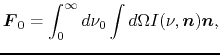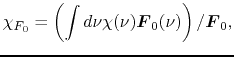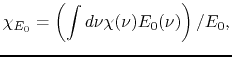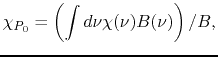The basic equation for gas which is affected by the radiation is as follows:
| |
|
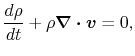 |
(D.1) |
| |
|
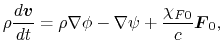 |
(D.2) |
| |
|
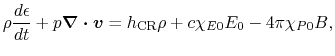 |
(D.3) |
| |
|
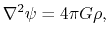 |
(D.4) |
| |
|
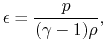 |
(D.5) |
where 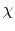 ,
, 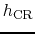 , and
, and 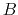 are the absorption coefficient,
the cosmic-ray heating rate perunit mass, and teh Planck function
are the absorption coefficient,
the cosmic-ray heating rate perunit mass, and teh Planck function
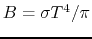 .
In equation (D.2), the term
.
In equation (D.2), the term
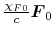 represents
the acceleration of gas due to the photon pressure.
In equation (D.3),
represents
the acceleration of gas due to the photon pressure.
In equation (D.3),
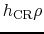 ,
, 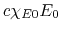 and
and
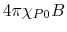 represent, respectively the heating due to the CR particles,
heating due to the absorption of radiation and cooling die to the emission.
The frequence-integrated radiation energy density and radiation flux are defined as
represent, respectively the heating due to the CR particles,
heating due to the absorption of radiation and cooling die to the emission.
The frequence-integrated radiation energy density and radiation flux are defined as
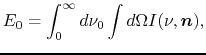 |
|
|
(D.6) |
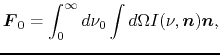 |
|
|
(D.7) |
where
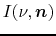 denotes the specific intensity of radiation at frequency
denotes the specific intensity of radiation at frequency 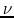 along the direction vector
along the direction vector 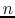 .
These equation could be solved if the the radiation transfer is solved.
The frequency-averaged absorption coefficients are defined as follows:
.
These equation could be solved if the the radiation transfer is solved.
The frequency-averaged absorption coefficients are defined as follows:
While the equation for the radiation transfer is basically as follows:
![\begin{displaymath}
\frac{1}{c}\frac{\partial I(\nu,\mbox{\boldmath${r}$},\mbox{...
...$},\mbox{\boldmath${n}$})-S(\nu,\mbox{\boldmath${r}$})\right],
\end{displaymath}](img1751.png) |
(D.11) |
where
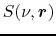 represent the source term.
represent the source term.
Kohji Tomisaka
2009-12-10