In this section, we will show the basic equation describing how the gravity works.
First, compare the gravity and the static electric force.
Consider the electric field formed by a point charge 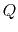 at a distance
at a distance 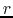 from the point source as
from the point source as
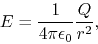 |
(2.6) |
where 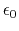 is the electric permittivity of the vacuum.
On the other hand, the gravitational acceleration by the point mass of
is the electric permittivity of the vacuum.
On the other hand, the gravitational acceleration by the point mass of 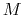 at the distance
at the distance 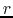 from the point mass is written down as
from the point mass is written down as
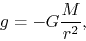 |
(2.7) |
where
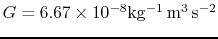 is the gravitational constant.
Comparing these two, replacing
is the gravitational constant.
Comparing these two, replacing 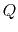 with
with 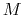 and at the same time
and at the same time
 to
to 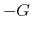 these equations (2.6) and (2.7) are identical with each other.
these equations (2.6) and (2.7) are identical with each other.
The Gauss theorem for electrostatic field as
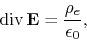 |
(2.8) |
and another expression using the electrostatic potential 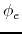 as
as
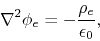 |
(2.9) |
lead to the equations for the gravity as
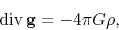 |
(2.10) |
and
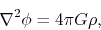 |
(2.11) |
where 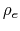 and
and 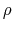 represent the electric charge density and the mass density.
Equation (2.11) is called the Poisson equation for the gravitational potential and describes
how the potential
represent the electric charge density and the mass density.
Equation (2.11) is called the Poisson equation for the gravitational potential and describes
how the potential 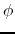 is determined from the mass density distribution
is determined from the mass density distribution 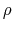 .
.
Subsections
Kohji Tomisaka
2009-12-10
![]() at a distance
at a distance ![]() from the point source as
from the point source as