Next: Steady State Flow under Up: Super- and Subsonic Flow Previous: Super- and Subsonic Flow Contents
 |
| (2.85) |
In the supersonic regime ![]() ,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (
,
the factor in the parenthesis of the lhs of equation (2.88) is positive.
This leads to the fact that the velocity increases (![]() ) as long as the cross-section increases (
) as long as the cross-section increases (![]() ).
On the other hand, in the subsonic regime, the velocity decreases (
).
On the other hand, in the subsonic regime, the velocity decreases (![]() )
while the cross-section increases (
)
while the cross-section increases (![]() ).
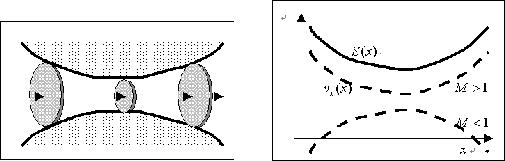
See right panel of 2.5.
).
See right panel of 2.5.
If ![]() at the point of minimum cross-section (throat), two curves for
at the point of minimum cross-section (throat), two curves for ![]() and
and ![]() have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.
have an
intersection.
In this case, gas can be accelerated through the Laval nozzle.
First, a subsonic flow is accelerated to the sonic speed at the throat of the nozzle.
After passing the throat, the gas follows the path of a supersonic flow, where the velocity is accelerated as long as
the cross-section increases.
Kohji Tomisaka 2009-12-10