Next: Group Velocity Up: Galactic Scale Star Formation Previous: Spiral Structure Contents
 |
We have derived the dispersion relation of the gravitational instability in the rotating thin disk as
| (3.37) |
| (3.40) |
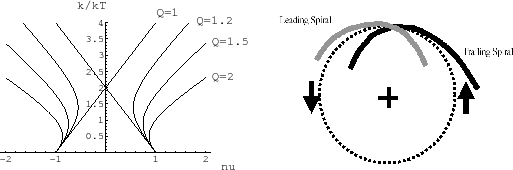
Plotting the wavenumber ![]() against the normalized frequency
against the normalized frequency ![]() of
equation (3.39) as Figure 3.11(left),
it is shown that, in the case of
of
equation (3.39) as Figure 3.11(left),
it is shown that, in the case of ![]() , the wavenumber exists for all
, the wavenumber exists for all ![]() .
Since
.
Since ![]() , 0, and +1 correspond to the points of ILR, CR, and OLR and these three resonance points
appear in accordance with the radial distance, the
, 0, and +1 correspond to the points of ILR, CR, and OLR and these three resonance points
appear in accordance with the radial distance, the ![]() -axis of Figure 3.11(left)
seems to correspond to the radial distance from the center.
In the case of
-axis of Figure 3.11(left)
seems to correspond to the radial distance from the center.
In the case of ![]() , it is shown that a forbidden region appears around the co-rotation resonance point.
Waves cannot propagate into the region.
Figure 3.11(left) shows that
the
, it is shown that a forbidden region appears around the co-rotation resonance point.
Waves cannot propagate into the region.
Figure 3.11(left) shows that
the ![]() has two possible wavenumbers in the permitted region.
The waves with larger
has two possible wavenumbers in the permitted region.
The waves with larger ![]() and smaller
and smaller ![]() are called short waves and long waves, respectively.
are called short waves and long waves, respectively.
Consider a wave expressed by
![]() .
If
.
If ![]() , moving from a point
, moving from a point ![]() in the direction
in the direction ![]() and
and ![]() the phase difference between the two points
the phase difference between the two points
![]() can be equal to zero.
That is, in the case of
can be equal to zero.
That is, in the case of ![]() the wave is leading.
On the other hand, if
the wave is leading.
On the other hand, if ![]() , moving in the direction
, moving in the direction ![]() and
and ![]() the phase
will be unchanged.
In this case, the wave pattern is trailing.
Since the dispersion relation is symmetric for
the phase
will be unchanged.
In this case, the wave pattern is trailing.
Since the dispersion relation is symmetric for ![]() and
and ![]() , there are two waves, trailing waves and
leading waves.
Therefore there are four waves: a short trailing wave, a long trailing wave,
a short leading wave, and a long leading wave.
, there are two waves, trailing waves and
leading waves.
Therefore there are four waves: a short trailing wave, a long trailing wave,
a short leading wave, and a long leading wave.