Bonnor-Ebert Mass

In the preceding section [Fig.4.1 (left)], we have seen the radial density distribution of a hydrostatic configuration of an isothermal gas. Consider a circumstance that such kind of cloud is immersed in a low-density medium with a pressure $p_0$. To establish a pressure equilibrium, the pressure at the surface $c_{\rm is}^2\rho(R)$ must equal to $p_0$. This means that the density at the surface is constant $\rho(R)=p_0/c_{\rm is}^2$.

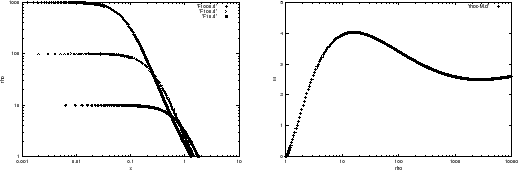
Figure 4.2 (left) shows three models of density distribution, $\rho_c=\rho(r=0)=10 \rho_s$, $10^2\rho_s$, and $10^3\rho_s$. Comparing these three models, it should be noticed that the cloud size (radius) decreases with increasing the central density $\rho _c$. The mass of the cloud is obtained by integrating the distribution, which is illustrated against the central-to-surface density ratio $\rho_c/\rho_s$ in Figure 4.2 (right). The $y$-axis represents a normalized mass as $m=M/[4\pi \rho_s (c_{\rm is}/\sqrt{4\pi G \rho_s})^3]$. The maximum value of $m=4.026$ means

$$M_{\rm max}\simeq 1.14 \frac{c_{\rm is}^2}{G^{3/2} p_0^{1/2}}.$$ (4.9)

This is the maximum mass which is supported against the self-gravity by the thermal pressure with an isothermal sound speed of $c_{\rm is}$, when the cloud is immersed in the pressure $p_0$. This is called Bonnor-Ebert mass [Bonnor (1956), Ebert (1955)]. It is to be noticed that the critical state $M_{\rm cl}=M_{\rm max}$ is achieved when the density contrast is rather low $\rho_c\simeq 16\rho_s\equiv \rho_{\rm cr}$.

Another important result from Figure 4.2 (right) is the stability of an isothermal cloud. Even for a cloud with $M_{\rm cl} < M_{\rm max}$, any clouds on the part of $\partial M_{\rm cl}/\partial \rho_c <0$ are unstable, whose clouds are distributed on the branch with $\rho_c >\rho_{\rm cr}$. This is understood as follows: For a hydrostatic cloud the mass should be expressed with the external pressure and the central density [Fig.4.2 (right)] as

$$M_{\rm cl}=M_{\rm cl}(p_{\rm ext},\rho_c).$$ (4.10)

In this case, a relation between the partial derivatives such as

$$\left(\frac{\partial M_{\rm cl}}{\partial p_{\rm ext}}\righ... ...artial \rho_c}{\partial M_{\rm cl}}\right)_{p_{\rm ext}}=-1,$$ (4.11)

is satisfied, unless each term is equal to zero. Figure 4.1 (left) shows that the cloud mass $M_{\rm cl}$ is a decreasing function of the external pressure $p_{\rm ext}=\rho_s c_{\rm is}^2$, if the central density is fixed. Since this means

$$\left(\frac{\partial M_{\rm cl}}{\partial p_{\rm ext}}\right)_{\rho_c}<0,$$ (4.12)

equation (4.11) gives us

$$\left(\frac{\partial p_{\rm ext}}{\partial \rho_c}\right)_{... ...rtial \rho_c}{\partial M_{\rm cl}}\right)_{p_{\rm ext}} > 0.$$ (4.13)

For a cloud with $\rho_c < \rho_{\rm cr}=16 p_{\rm ext}/c_{\rm is}^2$ the mass is an increasing function of the central density as

$$\left(\frac{\partial M_{\rm cl}}{\partial \rho_c}\right)_{p_{\rm ext}}>0.$$ (4.14)

Thus, equation (4.13) leads to the relation

$$\left(\frac{\partial \rho_c}{\partial p_{\rm ext}}\right)_{M_{\rm cl}}>0,$$ (4.15)

for $\rho < \rho_{\rm cr}$. This means that gas cloud contracts (the central density and pressure increase), when the external pressure increases. This is an ordinary reaction of a stable gas.

On the other hand, the cloud on the part of $\left(\partial M_{\rm cl}/\partial \rho_c \right)_{p_{\rm ext}}<0$ (for $16 \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} \rho_... ...}^2)\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 2000$) behaves

$$\left(\frac{\partial \rho_c}{\partial p_{\rm ext}}\right)_{M_{\rm cl}} < 0,$$ (4.16)

and this represents that an extra external pressure decreases the central density and thus the pressure. Pressure encourages expansion. This reaction is unstable.

Figure 4.2: (Left) radial density distribution. Each curve has different $\rho _c$. The x-axis denotes the radial distance normalized by a scale-length as $c_{\rm is}^2/\sqrt{4\pi G p_{\rm ext}}$. It is shown that the radius increases with decreasing $\rho _c$ in this range ( $\rho_c=(10,10^2,10^3)\times p_{\rm ext}/c_{\rm is}^2$). (Right) The relation between mass ($M_{\rm cl}$) and the central density ($\rho _c$) is plotted, under the condition of constant external pressure. The x-axis represents the central density normalized by $\rho_s\equiv p_{\rm ext}/c_{\rm is}^2$. The y-axis represents the cloud mass normalized by $4\pi \rho_s (c_{\rm is}/\sqrt{4\pi G \rho_s})^3$.