Next: Star Formation Time Scale Up: Dynamical Collapse Previous: Inside-out Collapse Solution Contents
What is a protostellar core formed in a supercritical cloud/cloud core?
Is this different from the inside-out solution of Shu (1977)?
A solution which corresponds to the protostellar core is obtained by Hunter (1977) and
Whitworth and Summers (1985).
This is a solution with ![]() in equation (4.69).
The asymptotic behaviors of the density and infall velocity reaching the center
are different from that of the Larson-Penston self-similar solution for a prestellar collapse.
That is,
in equation (4.69).
The asymptotic behaviors of the density and infall velocity reaching the center
are different from that of the Larson-Penston self-similar solution for a prestellar collapse.
That is,
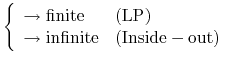 |
(4.91) | ||
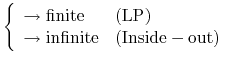 |
(4.92) |
Take notice that the solutions of ![]() (prestellar) and
(prestellar) and ![]() (protostellar) agree with each other at
(protostellar) agree with each other at ![]() .
Even if the boundary conditions at the center for the similarity variables,
.
Even if the boundary conditions at the center for the similarity variables, ![]() and
and ![]() , are completely different,
the difference between the two is small in the physical variable
, are completely different,
the difference between the two is small in the physical variable ![]() and
and ![]() .
Therefore, the evolution of a supercritical core is thought to be expressed by the Larson-Penston self-similar solution
extended to the protostellar core phase by Hunter (1977) and Whitworth and Summers (1985).
.
Therefore, the evolution of a supercritical core is thought to be expressed by the Larson-Penston self-similar solution
extended to the protostellar core phase by Hunter (1977) and Whitworth and Summers (1985).
Assume that we observe a protostellar core and obtain their density and infall velocity spatial distributions.
Can we distinguish which solution is appropriate for the Shu's inside-out solution or the extended Larson-Penston solution?
This seems hard, because the structure of density and velocity distributions are similar after the protostar is formed:
the density and velocity show almost similar power-law as
![]() and
and
![]() irrespective of the inside-out solution or the extended Larson-Penston solution.
The region where the infall velocity is accelerated toward the center (accretion-dominated region) is expanding
after the protostar is formed.
Therefore, to distinguish between the two solutions becomes harder and harder after the protostar is formed.
The difference would be large and we would have a definite answer which solution is appropriate to describe the cloud collapse,
if we can observe a very young protostellar core or a preprotostellar core which shows dynamical collapse.
However, since the time-scale of such a phase is much shorter than the evolved protostellar phase or a younger preprotostellar core,
the number of such kind of objects would be small (
irrespective of the inside-out solution or the extended Larson-Penston solution.
The region where the infall velocity is accelerated toward the center (accretion-dominated region) is expanding
after the protostar is formed.
Therefore, to distinguish between the two solutions becomes harder and harder after the protostar is formed.
The difference would be large and we would have a definite answer which solution is appropriate to describe the cloud collapse,
if we can observe a very young protostellar core or a preprotostellar core which shows dynamical collapse.
However, since the time-scale of such a phase is much shorter than the evolved protostellar phase or a younger preprotostellar core,
the number of such kind of objects would be small (
![]() ).
Therefore, we are looking for such objects just before or after the protostar formation.
).
Therefore, we are looking for such objects just before or after the protostar formation.
Kohji Tomisaka 2009-12-10