Next: Non-Local Thermal Equilibrium Up: Relation of Einstein's Coefficients Previous: Relation of Einstein's Coefficients Contents
Analysis using the Einstein's coefficients is applicable to the state in which the thermal equilibrium is not achieved. However, if this is applied to the thermal equilibrium, we can obtain relations between these coefficients.
Assume the detailed balance is achieved between
the spontaneous emission, the induced emission and the absorption as
Equation (2.148) gives
| (2.150) |
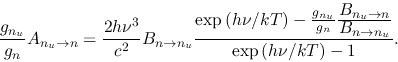 |
(2.152) |
| (2.153) |
Kohji Tomisaka 2012-10-03