Galactic Shock

In the preceding section, we have seen that a spiral pattern of density perturbation is made by the gravitational instability in the stellar system with $Q\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 1$. This forms a grand design spiral observed in the $I$-band images which represent the mass distribution which consists essentially in less-massive stars. The amplitude of the pattern is smaller than that observed in $B$-band images. In this section we will see how the distribution early type stars is explained. [Recommendation for a reference book of this section: Spitzer (1978).]

Figure 3.12: Spiral coordinate. Along a curve of constant $\eta$, $r\propto \exp(\theta \tan i)$.

Gas flowing through a spiral gravitational potential, even if its amplitude is relatively small, acts rather nonlinearly. Consider the gravitational potential in the sum of an axisymmetric term, $\Phi_0(R)$ and a spiral term $\Phi_1(R)$. The spiral gravitational field is rotating with a pattern speed $\Omega_{\rm P}$. We use a reference frame rotating with $\Omega_{\rm P}$. ${\bf u}=(u,v)$, where $u$ and $v$ are radial ($R$) and azimuthal ($\phi$) component of the flow velocity. Consider the reference system rotating with the angular rotation speed $\Omega_{\rm P}$. We assume the variables with suffix 0 represent those without the spiral potential $\Phi_1$ and variables with suffix 1 are used to express the difference between before and after $\Phi_1$ is added. $u=u_0+u_1=0+u_1$, $v=v_0+v_1$, and

$$v_0=R(\Omega-\Omega_{\rm P})=R\left[\left(\frac{1}{R}\frac{... ...ial \Phi_0}{\partial R}\right)^{1/2}-\Omega_{\rm P}\right],$$ (3.42)

where $\Omega$ means the circular rotation speed. The equation of motion in the $r$-direction is

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r... ...\partial r}-\frac{\partial \Phi_1}{\partial r}+2\Omega v_1,$$ (3.43)

and that in the $\phi$ direction is

$$\frac{\partial v}{\partial t}+u\left(\frac{\partial v_1}{\p... ...rtial \Phi_1}{\partial \phi} - \frac{\kappa^2}{2\Omega}u,$$ (3.44)

and the continuity equation is

$$\frac{\partial \Sigma R u}{\partial R}+\frac{\partial \Sigma v}{\partial \phi}=0.$$ (3.45)

As seen in Figure 3.12, we introduce the spiral coordinate $(\eta, \xi)$ in which $\xi$-axis is parallel to the spiral pattern which has a pitch angle $i$ and $\eta$-axis is perpendicular to the $\xi$-axis.

$$rd\eta = dr \cos i +r d\phi \sin i,$$ (3.46)

$$rd\xi = -dr \sin i + r d\phi \cos i.$$ (3.47)

$$v_\eta = u\cos i + v \sin i,$$ (3.48)

$$v_\xi = -u\sin i + v \cos i$$ (3.49)

Assuming that $i \ll 1$ (tightly wound spiral), equations (3.45) (3.43) and (3.44) become

$$\frac{\partial v_\eta}{\partial t}+v_\eta\frac{\partial v_\... ...artial \Phi_1}{\partial \eta} +2\Omega (v_\xi-v_{\xi 0}),$$ (3.50)

$$\frac{\partial v_\xi}{\partial t}+v_\eta\frac{\partial v_\x... ...partial \eta}=-\frac{\kappa^2}{2\Omega}(v_\eta-v_{\eta 0}),$$ (3.51)

$$\frac{\partial \Sigma}{\partial t}+\frac{\partial \Sigma v_\eta}{\partial \eta}=0.$$ (3.52)

Similar to $\S$2.8 we look for a steady state solution. Equation (3.52) becomes

$$\frac{d \Sigma}{d \eta}=-\frac{\Sigma}{v_\eta}\frac{d v_\eta}{d \eta}.$$ (3.53)

Using this, equation (3.50) reduces to

$$\left(v_\eta^2-c_s^2\right)\frac{d v_\eta}{d \eta}=2\Omega (v_\xi - v_{\xi 0})-\frac{d \Phi_1}{d \eta}.$$ (3.54)

Equation (3.51) becomes

$$v_\eta\frac{d v_\xi}{d \eta}=-\frac{\kappa^2}{2\Omega}(v_\eta-v_{\eta 0}).$$ (3.55)

In these equations we used following quantities:

$$v_\eta = v_{\eta 0}+v_{\eta 1},$$ (3.56)

$$v_\xi = v_{\xi 0}+v_{\xi 1},$$ (3.57)

$$v_{\eta 0} = v_0\sin i,$$ (3.58)

$$v_{\xi 0} = v_0\cos i,$$ (3.59)

$v_0$ is given in equation (3.42).

Equations (3.53), (3.54), and (3.55) are solved under the periodic boundary condition: $X(\eta={\rm right end})=X(\eta={\rm left end})$. Since equation (3.54) is similar to the equations in $\S$2.8, you may think the solution seems like Figure 2.6. However, it contains a term which expresses the effect of Coliois force $2\Omega (v_\xi - v_{\xi 0})$, the flow becomes much complicated.

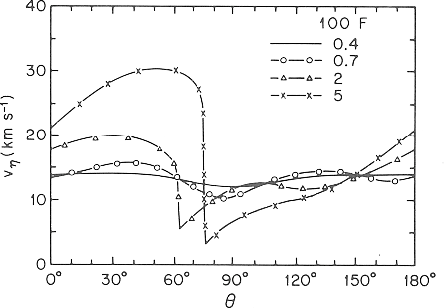
Taking care of the point that a shock front exists for a range of parameters, the solution of the above equations are shown in Figure 3.13. Numerical hydrodynamical calculations which solve equations (3.50), (3.51), and (3.52) was done and steady state solutions are obtained (Woodward 1975). It is shown that $F\le 0.7$%, the velocity ($v_\eta$: velocity perpendicular to the wave) does not show any discontinuity. In contrast, for $F>2$%, a shock wave appears. Steady state solution is obtained from the ordinary differential equations (3.53) (3.54), and (3.55) by Shu, Milione, & Roberts (1973). Inside the CR, $v_0 > 0$ (Gas has a faster rotation speed than the spiral pattern). As long as $v_\eta > c_s$ there is no shock. Increasing the amplitude of the spiral force $F$, an amplitude of the variation in $v_\eta$ increases and finally $v_\eta$ becomes subsonic partially. When the flow changes its nature from supersonic to subsonic, it is accompanied with a shock. (An inverse process, that is, changing from subsonic to supersonic is not accompanied with a shock.)

In the outer galaxy (still inside CR) since $\Omega-\Omega_{\rm P}$ decreases with the the distance from the galactic center, $v_{\eta 0}= R(\Omega-\Omega_{\rm P})\sin i$ decreases. In this region, $v_{\eta 0}< c_{is}$ and the flow is subsonic if there is no spiral gravitational force, $F=0$. In such a circumstance, increasing $F$ amplifies the variation in $v_\eta$ and $v_\eta$ finally reaches the sound speed. Transonic flow shows again a shock.

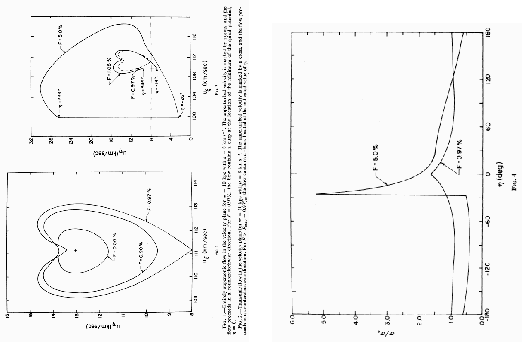
Summary of this section is:

1. There exists a spiral density pattern of the stellar component if the Toomre's $Q$ parameter is $1\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} Q \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 2$.
2. This is driven by the self-gravity of the rotating thin disk.
3. If the amplitude of the non-axisymmetric force is as large as $\sim 1$% of the axisymmetric one, interstellar gas whose sound speed is as large as $c_{is} \sim 8{\rm km s}^{-1}$ forms the galactic shock. This is observed when the flow is transonic.
4. The amplitude of the gas density fluctuation is much larger than that in the stellar density.
5. If stars are formed preferentially in the postshock region of the spiral arm, we expect clear spiral arms made by early-type stars, which are massive and short-lived, as seen in the $B$-band images of spiral galaxies.

Figure: Galactic shocks. The velocity perpendicular to the spiral wave front is plotted against the phase of the spiral wave. Gas flows from the left to the right. The spiral potential takes its minimum at $\theta=90\deg$. Parameters are taken as $c_s=8.6{\rm km s^{-1}}$, $i=6.\deg7$, $R=10$kpc, $R\Omega=250{\rm km s}^{-1}$, $R\kappa=313{\rm km s}^{-1}$, $R\Omega_{\rm P}=135{\rm km s}^{-1}$. The amplitude of spiral gravity force is taken $F=$0.4%, 0.7%, 2%, and 5% of the axisymmetric force $\partial \Phi _0/\partial R$. Taken from Fig.13.3 of Spizer (1978) [originally Woodward (1975)].

Figure 3.14: Galactic shock. (Left:) $v_\eta$ vs $v_\xi$ plot. Increasing $F$ from 0.5% to 0.9%, the variation in $v_\eta$ increases. And at $F=0.97$%, the minimum speed reaches the sound speed $8{\rm km s^{-1}}$. Further increasing $F$, a subsonic region appears ( $v_\eta < c_{is}$ for $F=1.05$% and 5%). When flow changes its nature from supersonic to subsonic, a shock appears. $R=10$kpc, $c_s=8{\rm km s}^{-1}$, and $i=6.\deg7$ are taken. Other parameters are the same as Fig.3.13. (Right:) Comparison of two density distributions: there are no shocks only cusps for $F < 0.97$%, while shochs and high compressions in the postshock region appear for models with $F=5$%. Taken from Shu, Milione, & Roberts (1973).