Angular Momentum Transfer

In the axisymmetric case, the poloidal $(z,r)$ and toroidal $(\phi)$ components of the magnetic field $\mbox{\boldmath${B}$}$ and current $\mbox{\boldmath${j}$}$ are decoupled with each other. That is, the poloidal ($B_p$) and toroidal ($B_\phi$) magnetic fields are made by the toroidal ($j_\phi$) and poloidal ($j_p$) electric currents, respectively. As for the Lorentz force $\mbox{\boldmath${j\times B}$}$, the poloidal component comes from $j_\phi B_p$ or $j_p B_\phi$, while the toroidal component does from $\mbox{\boldmath${j}$}_p\mbox{\boldmath${\times B}$}_p$. Even if there is no toroidal magnetic field (thus no poloidal electric current), there exists the poloidal component of the Lorentz force, which acts as a pressure to counter-balance the self-gravity ($\S$4.2). On the other hand, the toroidal component of the Lorentz force appears only the case with the poloidal electric current and thus toroidal component of magnetic field $B_\phi$. This means that the angular momentum is transferred by the magnetic field only when $B_\phi$ exists. Equation (B.14) explains how the angular momentum density $\rho v_\phi r$ is transferred. The left-hand side of equation (B.14) represents the advection of the angular momentum density, while the right-hand side

$$\frac{r}{4\pi}\left[ \frac{1}{r}\frac{\partial}{\partial r}... ...rac{\mbox{\boldmath${B}$}_p}{4\pi}\right)\cdot\nabla(rB_\phi),$$ (4.100)

represents the torque exerted on the gas parcel.

Figure 4.14: Pole-on (left) and side (right) views of the magnetic field lines, which drive the outflow.

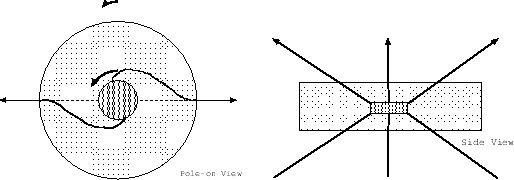The induction equation of the magnetic field [eq.(B.17)] shows that $B_\phi$ is generated from poloidal magnetic field by the effect of rotational motion $v_\phi$. This indicates that the angular momentum is transferred as follows:

1. The toroidal component of magnetic field $B_\phi$ is amplified by the dynamo process [equation (B.17)]. The magnetic field lines run like spiral viewing from the top like Figure 4.14.
2. Negative torque works near region attached to the fast-rotating disk, while positive one appears in the region connected to the radial magnetic field. The angular momentum is transferred from inside to outside along the same field line.
3. Angular momentum received by the gas near disk surface leads the excess centrifugal force which accelerate the gas. The disk inside which is affected by the negative torque loses its angular momentum and insufficient centrifugal force drives further accretion.

This angular momentum transfer on the same magnetic field has a character of angular momentum redistribution.