ベンチマークのページ

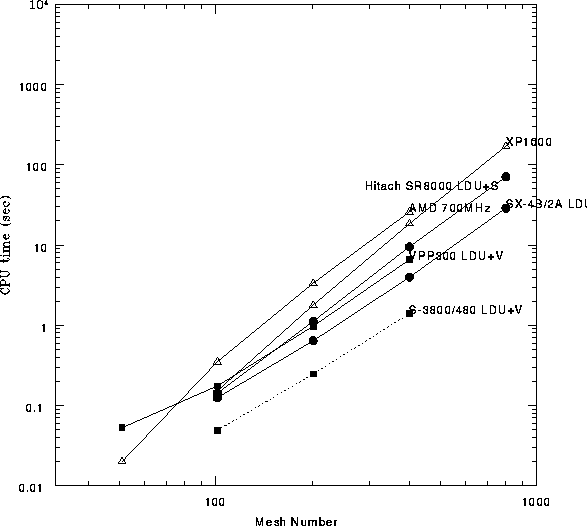
これは、２次元のポアソン方程式を、差分法によって解くスキームのうち、 非対称連立方程式を不完全LU分解で前処理して自乗共役勾配法(CGS)を もちいるもの(MICGS)について、ある精度まで解を求めるのに要する時間を 計測したものです。下にあるものほど高速ということになります。 １次元あたりの格子点数(N)を変化させた場合の時間の 変化をグラフにしています。ベクトル型のスーパーコンピュータと EWSのいくつかについて調べています。ここでは並列化についてはまったく 考えていません。参考：コンピュータによる連立１次方程式の解法（ ドンガラ他著、小国力訳、丸善）p.137およびpp.149-168。

ベクトル型のスーパーコンピュータ
■VPP300	富士通
■S820/80	日立
■S3800/480	日立
●SX-4B/2A	NEC

これらはいわゆるベクトル型のスーパーコンピュータです。 これらの機種では、不完全LU分解で前処理する部分をベクトル化する ためにリストベクトルを使ったコーディングがされています。

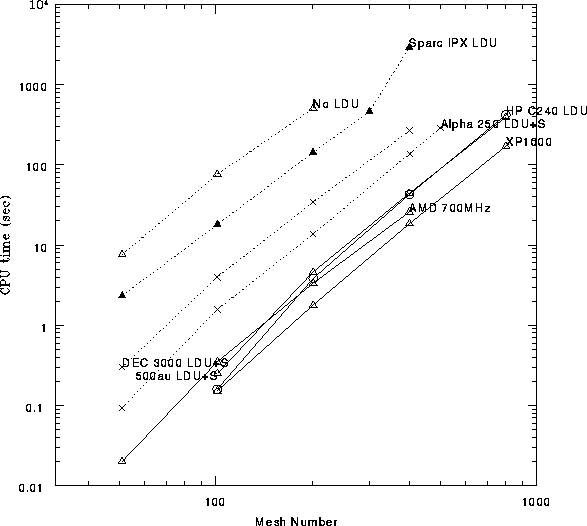
EWS
▲Sun SPARC IPX
×DEC Alpha 3000	αチップ21064(133MHz)
×DEC AlphaStation 250	21064A(266MHz)
△DEC Personal Workstation 500au	21164A(500MHz)
△Comaq Alpha Workstation XP1000	21264(500MHz)
○EWS4800/420	R5000SC(200MHz)
○HP C240
WinNT PC
×Dragon AXP 5/300	αチップ21164(300MHz)
△PC with AMD 700 MHz	AMD(700MHz)

これらはエンジニアリング・ワークステーションおよびパソコンです。 コンパイラはいずれもDigitalの機種についてはDEC Fortranによる。 これらのマシンでは不完全LU分解で前処理する部分はリストベクトルなど使わない コーディングがされています。

パソコンAMD(700MHz)とワークステーションα21264(500MHz)の差は、 ほぼ1.4倍に縮まっています。

興味のある方はソースを見て下さい。