宇宙背景放射から、宇宙に関する様々な情報を引き出すことができる。
たとえば、宇宙背景放射温度揺らぎの最初のピークと位置と振幅から、光子とバリオンが一流体とみなせる時代の音速やポテンシャルの変化の情報を引き出すことができる。
磁場があると流体の音速が増加し、ポテンシャルの時間進化にも影響を与えるため、宇宙背景放射の最初のピーク付近の観測データからも磁場の情報を引き出すことができる。
背景磁場の強度の宇宙全体での平均は0であるが、
背景磁場のエネルギー密度 (ρPMF) の宇宙全体での平均は有限である。
ビッグバン元素合成から制限した背景磁場のエネルギー密度(Yamazaki and Kusakabe, 2012)は、宇宙背景放射温度揺らぎの最初のピーク付近で無視できない影響を与えるのに十分な大きさであった。
インフレーション時に原初磁場が生成したと仮定した場合、そのスペクトルは、power law(冪乗則)で与えられる(参考:Yamazaki, et al. Phys. Rep. 517, 141, 2012)。
この場合、磁場のパラメータは、
コヒーレンススケール &lambda での磁場強度; Bλ
とスペクトル指数: nBである。
当研究では、パワーロウでスペクトルを与えた背景原初磁場の宇宙背景放射温度揺らぎに対する影響を、
背景原初磁場のパラメータごとに解析し、
標準的な宇宙論パラメータと背景原初磁場パラメータの縮退について初めて調査した。
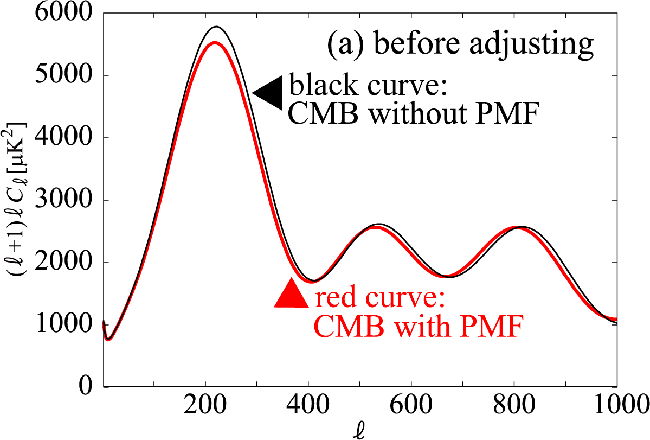
|
|
Fig. 1;
宇宙背景放射温度揺らぎに対する背景原初磁場と標準宇宙論パラメータの寄与。
図にマウスを重ねたさいに表示される図(b)は、
バリオン密度とコールドダークマター密度を調整したものである。
黒線は背景原初磁場の影響を考慮していない理論線。
赤線は背景原初磁場の影響を考慮した理論線で、背景原初磁場のパラメータは次の通りである:
(
nB, Bλ, kmax,ρMF/ργ) =
(-2.0, 10 nG, 1500 Mpc -1, 0.0160).
図(b)の赤線以外の標準宇宙論パラメータは、
(Ωb, ΩCDM, ns, 109Δ2R, H0, τ, r) = (0.0442, 0.210, 0.992, 2.26, 72.6, 0.091, 0.38)
である。
一方、図(b)の赤線で、ほかと異なるパラメータはバリオン密度とコールドダークマター密度で、その値は、(Ωb, ΩCDM) = (0.0461, 0.195)である。
|
背景原初磁場は、強結合した光子-バリオン流体の音速を増加させ、重力ポテンシャルの成長を阻害す。
結果として、背景原初磁場は、宇宙背景放射温度揺らぎの最初のピーク付近の振幅を小さくし、ピークの位置を大きいスケールへずらす[Fig. 1(a)]。
背景原初磁場のエネルギー密度は、最小スケールに依存し、その最小スケールは、背景原初磁場の生成モデルに依存する。
故に、背景原初磁場のエネルギー密度の制限から最小スケールを制限することができれば、背景原初磁場の生成モデルの情報を得ることができる。また、最小スケールを制限は、非線形領域の原初磁場の時間進化モデルの検証にも役立つ。
そこで、当研究では、背景原初磁場の最小スケールがフリーパラメータである場合も解析した。
その結果、背景原初磁場とバリオン密度の関係は、正相関であり、
ダークマターとは負相関であることがわかった。
[Fig. 1(a) and (b)].
これらの結果は、正しく原初磁場の初期宇宙における振る舞いを理解するためには、宇宙論的観測から背景原初磁場と標準宇宙論パラメータを同時に制限する必要があることを示している。
宇宙論的観測と当研究で修正された原初磁場のモデルを適用した理論計算を比較することにより原初磁場のパラメータを制限できれば、
その生成と時間進化のモデルのより正確に議論できるようになるであろう。
|
|

