Next: 端の運動 Up: Filament collapse: A two Previous: Filament collapse: A two
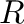 、密度
、密度
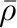 、長さ
、長さ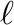 の等密度フィラメントの軸上の重力を計算する。
の等密度フィラメントの軸上の重力を計算する。
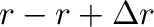 、
、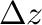 、
、
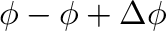 、
にある質量
、
にある質量
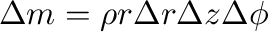 が
が
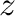 方向に
方向に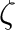 の距離に作る重力場は、図1左のように計算して、
の距離に作る重力場は、図1左のように計算して、
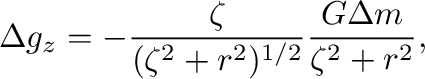 |
(1) |
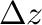 の円盤状の質量が
の円盤状の質量が
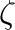 だけ離れた点に作る円盤に垂直な加速度成分は、
と書き表せる。ここで、
だけ離れた点に作る円盤に垂直な加速度成分は、
と書き表せる。ここで、
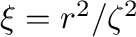 と置いた。
と置いた。
![\begin{figure}\centering
\includegraphics[bb=0 0 423 376,height=40mm]{grav.png}\hfil
\includegraphics[bb=0 0 281 383,height=40mm]{int.png}\end{figure}](img37.png) |
図1右でわかるように、
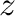 の位置の重力は、
の位置の重力は、
![$[z-\ell /2,z]$](img6.png) と
と
![$[z,\ell /2]$](img7.png) の部分は打ち消し合うので、
の部分は打ち消し合うので、
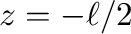 から
から
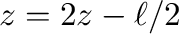 までの重力の合力となる。
式(2)で、
までの重力の合力となる。
式(2)で、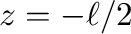 は
は
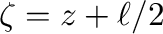 、
、
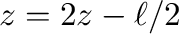 は
は
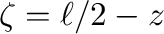 に対応するから、
に対応するから、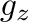 は
は
ここで、
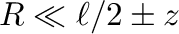 のもとに、これを展開して整理すると、以下のようになる。
のもとに、これを展開して整理すると、以下のようになる。
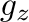 |
![$\displaystyle \simeq -2\pi G \bar{\rho}\left\{
2z+\left(\frac{\ell}{2}-z\right)...
...l}{2}+z\right)\left[1+\left(\frac{R}{\frac{\ell}{2}+z}\right)^2\right]
\right\}$](img47.png) |
|
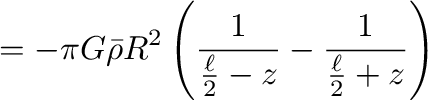 |
||
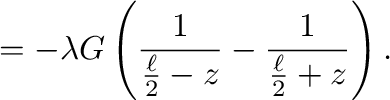 |
(4) |
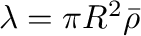 は、線質量を表す。
は、線質量を表す。
また、式(3)を
ここで、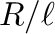 をパラメータとして、
をパラメータとして、
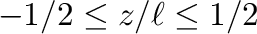 に対して、中括弧内を図示すると
図2のようになる。
端点に向かって重力加速度が増加する様子がわかる。
に対して、中括弧内を図示すると
図2のようになる。
端点に向かって重力加速度が増加する様子がわかる。
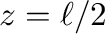 とすると、式(5)は、
とすると、式(5)は、
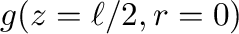 |
![$\displaystyle =-2\pi G \bar{\rho}\left[\ell-\left(\ell^2+R^2\right)^{1/2}+R\right]$](img57.png) |
|
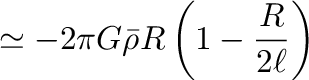 |
(6) |
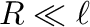 の場合、
の場合、
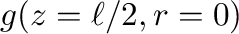 は
は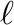 によらず、
によらず、
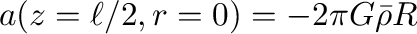 |
(7) |
![\begin{figure}\centering
\includegraphics[bb=0 0 360 226,height=40mm]{a_z.png}\hfil
\includegraphics[bb=0 0 559 386,height=40mm]{a_z_var.png}\end{figure}](img62.png) |
上記では一様密度
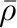 の円柱に働く自己重力を考察したが、
本論文では、様々な初期半径分布
の円柱に働く自己重力を考察したが、
本論文では、様々な初期半径分布
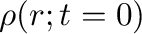 を検討している(図2右)。
等温平衡解はStod�kiewicz (1963)やOstriker (1964)により、
を検討している(図2右)。
等温平衡解はStod�kiewicz (1963)やOstriker (1964)により、
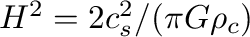 、で与えられているが、この解で
シャープに打ち切った
(図2右でOstriker)や、
(図2右でOstriker SE)を数値ポアソン方程式解法で解くと図2右のようになる。
、で与えられているが、この解で
シャープに打ち切った
(図2右でOstriker)や、
(図2右でOstriker SE)を数値ポアソン方程式解法で解くと図2右のようになる。