本論文では、数値ポアッソン解法と3次元流体コードRAMSESを用いた数値計算で
有限長さのフィラメントの収縮を調べているが、
ここでは、もう少し、解析的な取り扱いを進めてみる。
端に高密度のコアを形成するが、その運動は以下のようにして解析できる。
コアの質量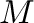 、速度
、速度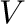 、コアの断面積を
、コアの断面積を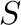 とすると、
コアはフィラメントの一様密度
とすると、
コアはフィラメントの一様密度
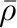 を降着させながら落下するので、
その質量変化は、
を降着させながら落下するので、
その質量変化は、
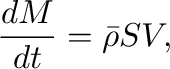 |
(11) |
一方、運動方程式は、
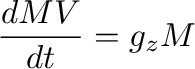 |
(12) |
で与えられる。以上2式から
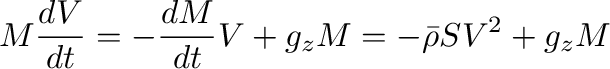 |
(13) |
あるいは、
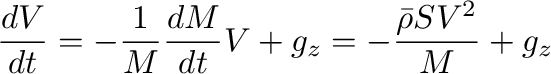 |
(14) |
が得られる。
式(13)及び式(14)の右辺第1項は、降着があたかも運動するコアに対するフィラメント内のガスのラム圧
によって減速を受けるのと同等に見えるように定式化されることがわかる
(著者らは先験的にラム圧が重要と提案しているが)。
図 3:
(左):
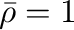 、
、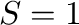 、
、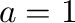 の場合の、速度
の場合の、速度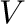 、位置
、位置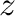 の時間変化。
2つの値の加速度を使って近似した、等加速度運動近似の速度を点線で示した。
(右): 同じく、質量
の時間変化。
2つの値の加速度を使って近似した、等加速度運動近似の速度を点線で示した。
(右): 同じく、質量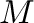 と運動量
と運動量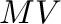 の時間変化。
の時間変化。
![\begin{figure}\centering
\includegraphics[bb=0 0 499 300,height=38mm]{v_z_t.png}\hfil
\includegraphics[bb=0 0 522 300,height=38mm]{m_mom_t.png}\end{figure}](img72.png) |
図3に、パラメータを
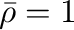 、
、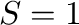 、
、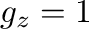 とし、
初期条件として、
とし、
初期条件として、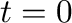 で、
で、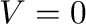 、
、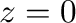 を取った場合の解を示した。
図3(左)に、速度
を取った場合の解を示した。
図3(左)に、速度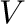 が、近似的に一定の加速度で加速される2つの等加速度運動
でよく近似できることを示した。
が、近似的に一定の加速度で加速される2つの等加速度運動
でよく近似できることを示した。
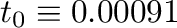 として、
として、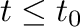 では、
では、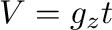 の重力加速度
の重力加速度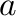 による等加速度運動、
その後の
による等加速度運動、
その後の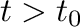 では、別の加速度
では、別の加速度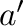 による
による
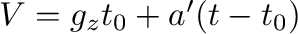 の重力加速度による等加速度運動、すなわち、
の重力加速度による等加速度運動、すなわち、
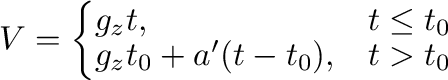 |
(15) |
で、よく近似できる(図3の破線)。
 に対して、
に対して、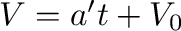 を式(11)に代入すると、
を式(11)に代入すると、
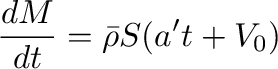 |
(16) |
から
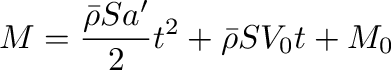 |
(17) |
のように求められる。
式(14)は、
となるが、分母、分子の3項目が1、2項目に比べて無視できれば、
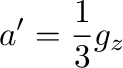 |
(19) |
となるが、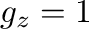 の場合、図3の破線の傾きは
の場合、図3の破線の傾きは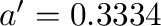 で、数値的にもよく再現されている。
で、数値的にもよく再現されている。
著者らは、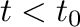 は等加速度運動だが、
は等加速度運動だが、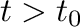 は等速直線運動であると述べているが、
果たしてそうなのであろうか。
ニュートン則(摩擦抵抗が速度の2乗に比例する抵抗則)が成り立つ物体の
一定重力加速度での落下の場合、
終端速度へ漸近と、その後の等速運動が知られるが、それは質量
は等速直線運動であると述べているが、
果たしてそうなのであろうか。
ニュートン則(摩擦抵抗が速度の2乗に比例する抵抗則)が成り立つ物体の
一定重力加速度での落下の場合、
終端速度へ漸近と、その後の等速運動が知られるが、それは質量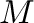 が
一定であるからで、この降着を伴う重力収縮では、漸近的に一定加速度の運動をし、
その加速度は
が
一定であるからで、この降着を伴う重力収縮では、漸近的に一定加速度の運動をし、
その加速度は
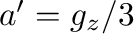 となるのではなかろうか。
となるのではなかろうか。
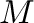 、速度
、速度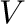 、コアの断面積を
、コアの断面積を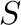 とすると、
コアはフィラメントの一様密度
とすると、
コアはフィラメントの一様密度
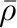 を降着させながら落下するので、
その質量変化は、
を降着させながら落下するので、
その質量変化は、
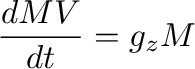
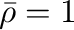 、
、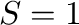 、
、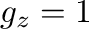 とし、
初期条件として、
とし、
初期条件として、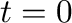 で、
で、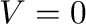 、
、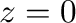 を取った場合の解を示した。
図3(左)に、速度
を取った場合の解を示した。
図3(左)に、速度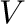 が、近似的に一定の加速度で加速される2つの等加速度運動
でよく近似できることを示した。
が、近似的に一定の加速度で加速される2つの等加速度運動
でよく近似できることを示した。
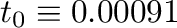 として、
として、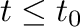 では、
では、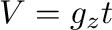 の重力加速度
の重力加速度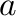 による等加速度運動、
その後の
による等加速度運動、
その後の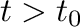 では、別の加速度
では、別の加速度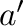 による
による
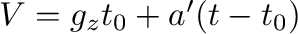 の重力加速度による等加速度運動、すなわち、
の重力加速度による等加速度運動、すなわち、
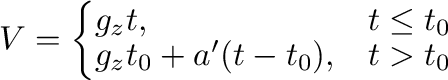
 に対して、
に対して、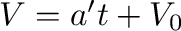 を式(11)に代入すると、
を式(11)に代入すると、
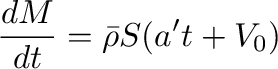
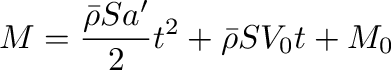
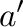
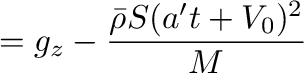
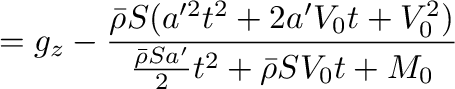
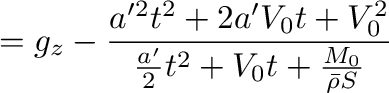
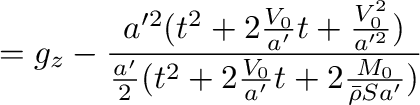
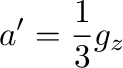
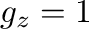 の場合、図3の破線の傾きは
の場合、図3の破線の傾きは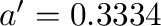 で、数値的にもよく再現されている。
で、数値的にもよく再現されている。
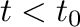 は等加速度運動だが、
は等加速度運動だが、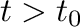 は等速直線運動であると述べているが、
果たしてそうなのであろうか。
ニュートン則(摩擦抵抗が速度の2乗に比例する抵抗則)が成り立つ物体の
一定重力加速度での落下の場合、
終端速度へ漸近と、その後の等速運動が知られるが、それは質量
は等速直線運動であると述べているが、
果たしてそうなのであろうか。
ニュートン則(摩擦抵抗が速度の2乗に比例する抵抗則)が成り立つ物体の
一定重力加速度での落下の場合、
終端速度へ漸近と、その後の等速運動が知られるが、それは質量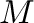 が
一定であるからで、この降着を伴う重力収縮では、漸近的に一定加速度の運動をし、
その加速度は
が
一定であるからで、この降着を伴う重力収縮では、漸近的に一定加速度の運動をし、
その加速度は
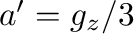 となるのではなかろうか。
となるのではなかろうか。