
固有値

を考える。
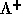 は
は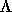 のうち正の固有値のみを持つ行列、
のうち正の固有値のみを持つ行列、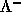 は負の
固有値のみを持つ行列である。
この速度でやりとりされる、流束の方も
は負の
固有値のみを持つ行列である。
この速度でやりとりされる、流束の方も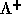 によって移動する
によって移動する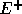 と
と
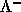 によって移動する
によって移動する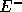 とに分離することを考える。
そこで、
とに分離することを考える。
そこで、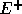 については後退差分を、
については後退差分を、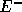 については前進差分をとれば
自然と風上差分が実現する。
この方法を、Flux vector Splitting(FVS:流速分離)法という。
については前進差分をとれば
自然と風上差分が実現する。
この方法を、Flux vector Splitting(FVS:流速分離)法という。
空間微分の項は
のように書ける。 ここで、流束は


のように計算される。
プログラムを見てみよう。
右固有行列RをR[l,m]に、
その逆行列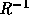 を
をL[l,m]に求めるところはFDSと同じである。
w[n1,n2]は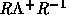 が格納される。
最後にこれに伴う数値流束
が格納される。
最後にこれに伴う数値流束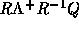 を
をEp[j]に求めている。
for n1:=1 to 3 do
begin
for n2:=1 to 3 do
begin
w[n1,n2]:=0.0;
for k:=1 to 3 do
begin
w[n1,n2]:=w[n1,n2]
+R[n1,k]*max(0.0,Lambda[k])*L[k,n2];
end;
end;
end;
E1p[j]:=w[1,1]*rho[j]+w[1,2]*m[j]+w[1,3]*e[j];
E2p[j]:=w[2,1]*rho[j]+w[2,2]*m[j]+w[2,3]*e[j];
E3p[j]:=w[3,1]*rho[j]+w[3,2]*m[j]+w[3,3]*e[j];
つぎに、
w[n1,n2]は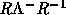 が格納される。
最後にこれに伴う数値流束
が格納される。
最後にこれに伴う数値流束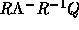 を
をEm[j]に求めている。
for n1:=1 to 3 do
begin
for n2:=1 to 3 do
begin
w[n1,n2]:=0.0;
for k:=1 to 3 do
begin
w[n1,n2]:=w[n1,n2]
+R[n1,k]*min(0.0,Lambda[k])*L[k,n2];
end;
end;
end;
E1m[j]:=w[1,1]*rho[j]+w[1,2]*m[j]+w[1,3]*e[j];
E2m[j]:=w[2,1]*rho[j]+w[2,2]*m[j]+w[2,3]*e[j];
E3m[j]:=w[3,1]*rho[j]+w[3,2]*m[j]+w[3,3]*e[j];
end;
ここで得られた数値流束は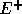 (
(Ep[j])については後退差分、
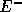 (
(Em[j])については前進差分をとって、
時間進化を計算することによって、
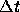 だけ進んだ状態を計算することができる。
だけ進んだ状態を計算することができる。
for j:=1 to jm-1 do
begin
rho[j]:=rho[j]-nu*(E1p[j]+E1m[j+1]-E1p[j-1]-E1m[j]);
m[j] :=m[j] -nu*(E2p[j]+E2m[j+1]-E2p[j-1]-E2m[j]);
e[j] :=e[j] -nu*(E3p[j]+E3m[j+1]-E3p[j-1]-E3m[j]);
end;
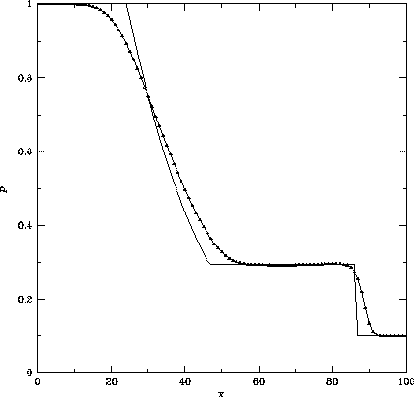
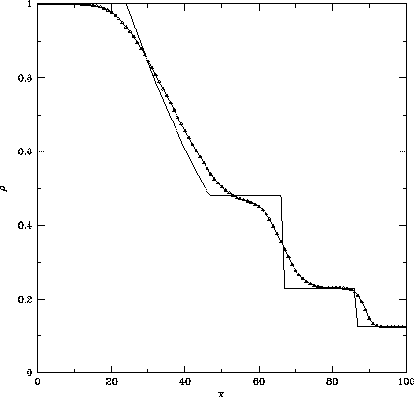
Figure 3.7: Steger WarmingのFlux Vector Splitting法による衝撃波管問題の解。
初期条件は同じ。