

に左固有行列(右固有行列の逆行列)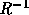 を左から掛けると、
を左から掛けると、

よって、Rが微小な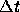 、
、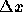 に関して一定とみなせるなら、
に関して一定とみなせるなら、

のように書ける。 ここで、風上差分の数値流束を
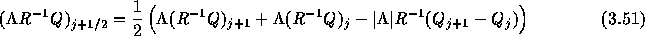
左からRを掛けると
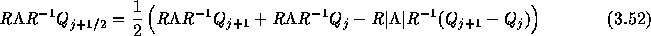
となるが、この式は
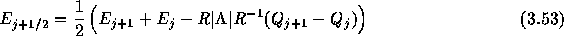
と書き直すことができて、 FDS(Flux Difference Spilitting)スキームの数値流速を与える。
ここで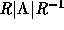 の項は
の項は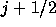 についての量なのであるが、
FDSスキームでは、Roeの近似リーマン解法を用いてこの中間値を評価する。
についての量なのであるが、
FDSスキームでは、Roeの近似リーマン解法を用いてこの中間値を評価する。
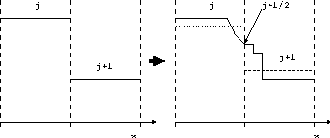
Figure 3.5: 近似リーマン解法の概念図。物理量がグリッドの内部で空間的に一定
だったとして、その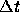 後の物理量の分布を解く。それが右の図のよ
うなものであった場合はそれをグリッドで1個で平均した量(右図の点線)
を
後の物理量の分布を解く。それが右の図のよ
うなものであった場合はそれをグリッドで1個で平均した量(右図の点線)
を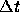 後のグリッドの物理量とする方法をGonunov法という。
これを使うと、
後のグリッドの物理量とする方法をGonunov法という。
これを使うと、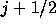 の物理量を正確に求めることができる。このように
して得た
の物理量を正確に求めることができる。このように
して得た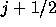 の物理量を風上差分の数値流束の評価に用いる方法を
近似リーマン解法を用いた差分法と呼ぶ。
の物理量を風上差分の数値流束の評価に用いる方法を
近似リーマン解法を用いた差分法と呼ぶ。
1次元の単純な衝撃波管問題(リーマン問題)の
解は解析的に得られる。
jおよびj+1のグリッドの時間tでの物理量がわかっていれば、その後の
解を正確にとくことができてこれを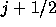 の物理量の評価に用いることがで
きる。
これを正確に解くのではなく、近似的に解いて(近似リーマン解法)
それを
の物理量の評価に用いることがで
きる。
これを正確に解くのではなく、近似的に解いて(近似リーマン解法)
それを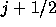 の物理量の評価に用いる。
Roeの近似リーマン解法と呼ばれるものは、
境界の左側の物理量
の物理量の評価に用いる。
Roeの近似リーマン解法と呼ばれるものは、
境界の左側の物理量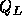 と右側の物理量
と右側の物理量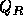 を用いて、平均の値
を用いて、平均の値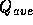 を
を




(Hは単位質量あたりの全エンタルピーで
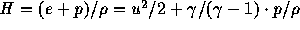 である)。
のように平均量(Roe平均)を得るものである。
である)。
のように平均量(Roe平均)を得るものである。
この評価式は、
(1)流束ヤコビアンに関する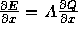 が
差分式についてもなり立つこと:
が
差分式についてもなり立つこと:
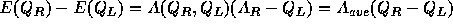 。
。
(2)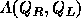 はAと同じように、実固有値と線形独立な固有ベクトルを持つこと。
はAと同じように、実固有値と線形独立な固有ベクトルを持つこと。
(3)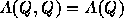 という対称性を持つこと。
という対称性を持つこと。
これら(Property U)を満たすものとしてRoeにより提案されたものである。
プログラムは、第1に
for j:=0 to jm-1 do // Roe Average
begin
rhop[j]:=Sqrt(rho[j]*rho[j+1]);
up[j]:=(Sqrt(rho[j])*u[j]+Sqrt(rho[j+1])*u[j+1])/(Sqrt(rho[j])+Sqrt(rho[j+1]));
Hp[j]:=(Sqrt(rho[j])*H[j]+Sqrt(rho[j+1])*H[j+1])/(Sqrt(rho[j])+Sqrt(rho[j+1]));
cp[j]:=Sqrt(gam1*(Hp[j]-up[j]*up[j]/2))
end;
でrhop[j]などにRoe平均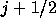 の評価値を求める。
次に、右固有行列Rを
の評価値を求める。
次に、右固有行列RをR[l,m]に、
その逆行列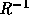 を
をL[l,m]に求める。
w[n1,n2]は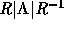 が格納される。
最後に数値流束を
が格納される。
最後に数値流束をE[j]に求めている。
for j:=0 to jm-1 do
begin
Lambda[1]:=Abs(up[j]-cp[j]);
Lambda[2]:=Abs(up[j]);
Lambda[3]:=Abs(up[j]+cp[j]);
R[1,1]:= 1;
R[1,2]:= 1;
R[1,3]:= 1;
R[2,1]:= up[j]-cp[j];
R[2,2]:= up[j];
R[2,3]:= up[j]+cp[j];
R[3,1]:= Hp[j]-up[j]*cp[j];
R[3,2]:= Sqr(up[j])/2;
R[3,3]:= Hp[j]+up[j]*cp[j];
b1:=gam1/2*Sqr(up[j]/cp[j]);
b2:=gam1/Sqr(cp[j]);
L[1,1]:= 0.5*(b1+up[j]/cp[j]);
L[1,2]:= -0.5*(1/cp[j]+b2*up[j]);
L[1,3]:= 0.5*b2;
L[2,1]:= 1-b1;
L[2,2]:= b2*up[j];
L[2,3]:= -b2;
L[3,1]:= 0.5*(b1-up[j]/cp[j]);
L[3,2]:= 0.5*(1/cp[j]-b2*up[j]);
L[3,3]:= 0.5*b2;
for n1:=1 to 3 do
begin
for n2:=1 to 3 do
begin
w[n1,n2]:=0.0;
for k:=1 to 3 do
begin
w[n1,n2]:=w[n1,n2]+R[n1,k]*Lambda[k]*L[k,n2];
end;
end;
end;
E1[j]:=0.5*(m[j+1]+m[j]
-w[1,1]*(rho[j+1]-rho[j])
-w[1,2]*(m[j+1]-m[j])
-w[1,3]*(e[j+1]-e[j]));
E2[j]:=0.5*(gam1*(e[j+1]+e[j])+gam3/2*(Sqr(m[j+1])/rho[j+1]+Sqr(m[j])/rho[j])
-w[2,1]*(rho[j+1]-rho[j])
-w[2,2]*(m[j+1]-m[j])
-w[2,3]*(e[j+1]-e[j]));
E3[j]:=0.5*(gamma*(e[j+1]*m[j+1]/rho[j+1]+e[j]*m[j]/rho[j])
-gam1/2*(Sqr(m[j+1]/rho[j+1])*m[j+1]+Sqr(m[j]/rho[j])*m[j])
-w[3,1]*(rho[j+1]-rho[j])
-w[3,2]*(m[j+1]-m[j])
-w[3,3]*(e[j+1]-e[j]));
end;
この数値流束を用いて時間進化を計算すれば良い。
for j:=1 to jm-1 do
begin
rho[j]:=rho[j]-nu*(E1[j]-E1[j-1]);
m[j]:=m[j]-nu*(E2[j]-E2[j-1]);
e[j]:=e[j]-nu*(E3[j]-E3[j-1]);
end;
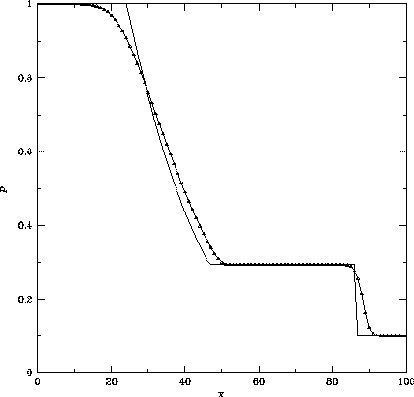
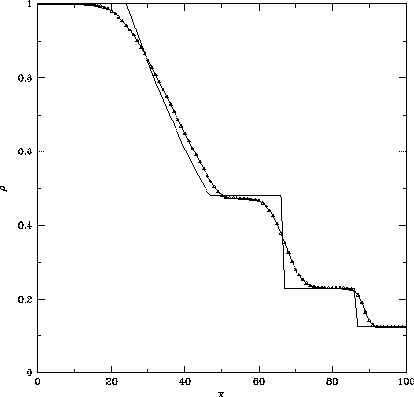
Figure 3.6: RoeのFlux Difference Splitting法による衝撃波管問題の解。
初期条件は同じ。