まず最初の基礎方程式は、 ある体積の中に含まれる流体の質量が単位時間に流れ込む 質量流速によって増減するという連続の式
から得られる。 右辺を体積積分に変換し、Vとして微小体積を考えれば、
が得られる。
つぎに、ある体積の中に含まれる流体の運動量は、質量と同じように、 単位時間に流れ込む運動量流速によって増減するが、それに加えて運動量の場合は、 この流体の体積に加わっている「力」によっても増減する。 流体の中でかならず考慮しなければならない圧力による力は、圧力勾配に 比例するので、
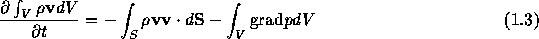
となる。 ここで、右辺を体積積分に変換し、Vとして微小体積を考えれば、
が得られる。 この式は添字をつけて書くと、
と書ける。もちろん、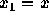
、
、
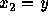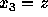を表している。
さて、断熱の場合のエネルギーに関する方程式は、
ここでeは単位体積あたりの全エネルギーで
第１項は単位体積当たりの
運動エネルギー、第２項はおなじく熱エネルギーを表す。
理想気体の場合は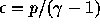 
である。
質量と同じように、全エネルギーの増減はエネルギー流速によるだけなら、
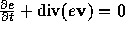となるはずであるが、そうではない。
熱力学の第１法則で断熱の場合を考えると、内部エネルギーUと
体積Vは
という関係で変化する。
これから、単位体積あたりの熱エネルギー
は
という関係にしたがって変化することが簡単な計算でわかる。 これと式(1.4)から得られる運動エネルギーの変化を表す （この式の右辺が単位体積・単位時間に流体素片になされた仕事を表すことに注意）
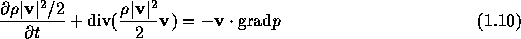
の和をとれば全エネルギーに関する方程式(1.6)が得られる。
流体力学の基礎方程式は、式(1.2)、(1.4)、 (1.6)ということになる。 １次元の流体の基礎方程式は、３つの式をベクトルのように並べて書いて、
と書ける ただし、QとEは物理量をならべたベクトルで、
である。
