


Next: Energy Equation
Up: Continuity Equation
Previous: Continuity Equation
Contents
It is useful to describe the equation for momentum
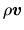 .
Eulerian derivative of momentum density
.
Eulerian derivative of momentum density
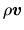 is rewritten as
is rewritten as
where we used equations (A.7)
and (A.11).
In the Cartesian cordinate
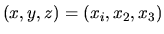 , this becomes
, this becomes
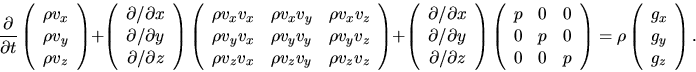 |
(A.13) |
Using the momentum stress tensor
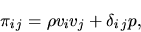 |
(A.14) |
the above equation is written as
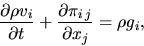 |
(A.15) |
where 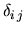 represents the Kronecker's delta as
represents the Kronecker's delta as
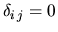 for
for 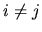 and
and
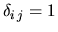 for
for 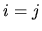 .
.
If there is no external force, rhs of equation (A.15)
is equal to zero.
If the momentum density
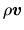 were to obey the continuity equation,
equation (A.15) would be
were to obey the continuity equation,
equation (A.15) would be
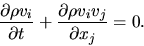 |
(A.16) |
However, this is incorrect, because there exists the pressure force
in the fluid and thus the momentum of the fluid element is not conserved.



Next: Energy Equation
Up: Continuity Equation
Previous: Continuity Equation
Contents
Kohji Tomisaka
2007-07-08
![]() .
Eulerian derivative of momentum density
.
Eulerian derivative of momentum density
![]() is rewritten as
is rewritten as
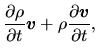
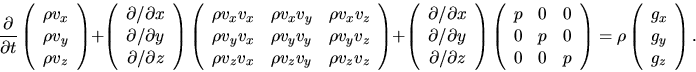
![]() were to obey the continuity equation,
equation (A.15) would be
were to obey the continuity equation,
equation (A.15) would be