


Next: Basic Equations of Magnetohydrodynamics
Up: Rankine-Hugoniot Relation
Previous: Rankine-Hugoniot Relation
Contents
In the case of the gas is isothermal
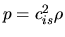 ,
equation (A.31) becomes
,
equation (A.31) becomes
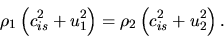 |
(A.32) |
Eliminating 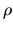 from equations (A.29) and (A.32), we obtain
from equations (A.29) and (A.32), we obtain
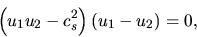 |
(A.33) |
which means
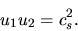 |
(A.34) |
From equation (A.29),
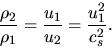 |
(A.35) |
This indicates the postshock velocity 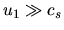 the ratio of the postshock density to the preshock
density becomes large.
the ratio of the postshock density to the preshock
density becomes large.
Kohji Tomisaka
2007-07-08
![]() ,
equation (A.31) becomes
,
equation (A.31) becomes