



Next: Axisymmetric Case
Up: Magnetohydrodynamics
Previous: Flux Freezing
Contents
Basic equations are as follows:
The mass continuity as
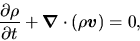 |
(B.7) |
the equation of motion as
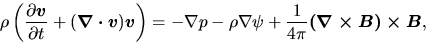 |
(B.8) |
the equation of thermal energy as
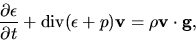 |
(B.9) |
or some barotropic relation 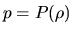 and the induction equation as
and the induction equation as
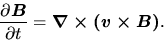 |
(B.10) |
Kohji Tomisaka
2007-07-08