



Next: Hydrostatic Equilibrium
Up: Magnetohydrodynamics
Previous: Basic Equations of Ideal
Contents
The basic equations to be solved are the magnetohydrodynamical equations
and the Poisson equation for the gravitational potential.
In cylindrical coordinates (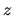 ,
, 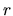 ,
, 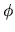 )
with
)
with
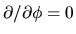 , the equations are expressed as follows:
, the equations are expressed as follows:
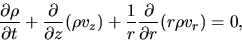 |
(B.11) |
![\begin{displaymath}
\frac{\partial \rho r v_\phi}{\partial t}+
\frac{\partial}...
...}(rB_\phi)B_r
+\frac{\partial B_\phi}{\partial z}B_z \right]
\end{displaymath}](img1473.png) |
(B.14) |
![\begin{displaymath}
\frac{\partial B_z}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}[r(v_zB_r-v_rB_z)],
\end{displaymath}](img1474.png) |
(B.15) |
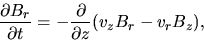 |
(B.16) |
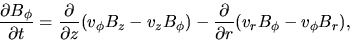 |
(B.17) |
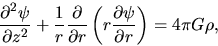 |
(B.18) |
where the variables have their ordinary meanings.
Equation (B.11) is the continuity equation;
equations (B.12), (B.13) and (B.14) are the
equations of motion.
The induction equations for the poloidal magnetic fields are
equations (B.15) and (B.16) and for the toroidal magnetic field
is equation (B.17).
The last equation (B.18) is the Poisson equation.




Next: Hydrostatic Equilibrium
Up: Magnetohydrodynamics
Previous: Basic Equations of Ideal
Contents
Kohji Tomisaka
2007-07-08
![]() ,
, ![]() ,
, ![]() )
with
)
with
![]() , the equations are expressed as follows:
, the equations are expressed as follows: