



Next: Rotating Disk
Up: Physical Background
Previous: Jeans Instability
Contents
Gravitational Instability of Thin Disk
Figure 2.3:
Thin disk.
 |
Disks are common in the Universe.
Spiral and barred spiral galaxies have disks where stars are formed.
In more small scale, gas and dust disks are often found around protostars.
Moreover, such a disk may become a proto-planetary disk.
It is valuable to study how the self-gravity works in such thin structures.
Here, we assume a thin disk extending in 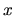 - and
- and 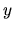 -directions
whose surface density is equal to
-directions
whose surface density is equal to
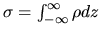 , in other word
the density is written using the Dirac's delta function
, in other word
the density is written using the Dirac's delta function 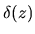 as
as
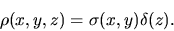 |
(2.55) |
Integrating along the 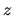 -direction basic equations
(2.45), (2.46), and (2.47),
the linearized basic equations for the thin disk are as follows:
-direction basic equations
(2.45), (2.46), and (2.47),
the linearized basic equations for the thin disk are as follows:
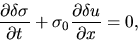 |
(2.56) |
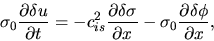 |
(2.57) |
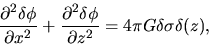 |
(2.58) |
where we assumed
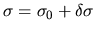 ,
, 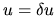 ,
,
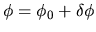 and took the first order terms (those contain only one
and took the first order terms (those contain only one 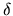 ).
).
Outside the disk, the rhs of equation (2.58) is equal to zero.
It reduces to the Laplace equation
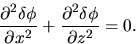 |
(2.59) |
Taking a plane wave of
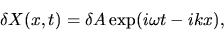 |
(2.60) |
equation (2.59) is reduced to
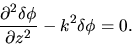 |
(2.61) |
This has a solution which does not diverge at the infinity 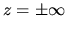 as
as
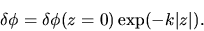 |
(2.62) |
On the other hand, integrating equation (2.58) from 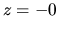 to
to 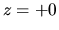 or in other word, applying the Gauss' theorem to the region containing the
or in other word, applying the Gauss' theorem to the region containing the 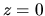 surface,
it is shown that the gravity
surface,
it is shown that the gravity
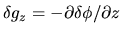 has a jump crossing the
has a jump crossing the 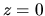 surface as
surface as
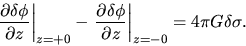 |
(2.63) |
Equations (2.62) and (2.63) lead a final form of the potential as
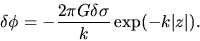 |
(2.64) |
Putting this to equations (2.57), and using equations (2.56) and
(2.57), we obtain the dispersion relation for the gravitational instability in a thin disk
as
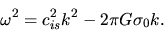 |
(2.65) |
This reduces to the dispersion relation of the sound wave for the short wave
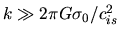 .
While for a longer wave than
.
While for a longer wave than
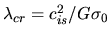 , an exponential growth of
, an exponential growth of 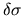 is expected.
The dispersion relation is shown in Fig.2.2.
is expected.
The dispersion relation is shown in Fig.2.2.
Subsections




Next: Rotating Disk
Up: Physical Background
Previous: Jeans Instability
Contents
Kohji Tomisaka
2007-07-08

![]() - and
- and ![]() -directions
whose surface density is equal to
-directions
whose surface density is equal to
![]() , in other word
the density is written using the Dirac's delta function
, in other word
the density is written using the Dirac's delta function ![]() as
as