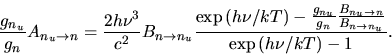


Next: Non-Local Thermal Equilibrium
Up: Relation of Einstein's Coefficients
Previous: Relation of Einstein's Coefficients
Contents
Analysis using the Einstein's coefficients is applicable to
the state in which the thermal equlibrium is not achieved.
However, if this is applied to the thermal equlibrium,
we can obtain relations between these coefficients.
Assume the detailed balance is achived between
the spontaneous emission, the induced emission and the absorption as
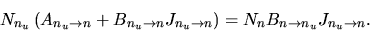 |
(2.144) |
In the thermal equlibrium,
the population of atoms is given by the Boltzmann distribution as
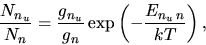 |
(2.145) |
where 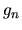 represents the statistical weight for the state n.
represents the statistical weight for the state n.
Equation (2.144) gives
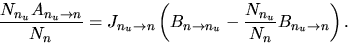 |
(2.146) |
In the case of thermal equilibrium, the average specific intensity
agrees with the Planck function 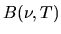 as
as
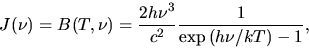 |
(2.147) |
Using equations (2.145) and (2.147),
equation (2.144) reduces to
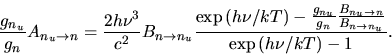 |
(2.148) |
Lefthabd-side of the equation is not dependent on the temperature.
For this equation to be valid for various temperature,
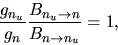 |
(2.149) |
and
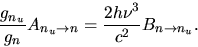 |
(2.150) |



Next: Non-Local Thermal Equilibrium
Up: Relation of Einstein's Coefficients
Previous: Relation of Einstein's Coefficients
Contents
Kohji Tomisaka
2007-07-08