



Next: Equilibria of Cylindrical Cloud
Up: Hydrostatic Balance
Previous: Problem 2
Contents
Bonnor-Ebert Mass
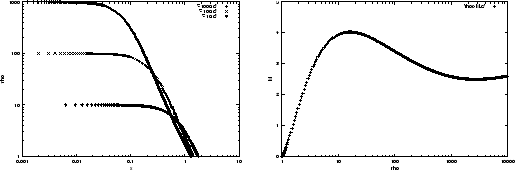
In the preceding section [Fig.4.1 (left)], we have seen the radial density distribution of
a hydrostatic configuration of an isothermal gas.
Consider a circumstance that such kind of cloud is immersed in a low-density medium with a pressure 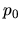 .
To establish a pressure equilibrium, the pressure at the surface
.
To establish a pressure equilibrium, the pressure at the surface
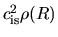 must equal to
must equal to 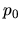 .
This means that the density at the surface is constant
.
This means that the density at the surface is constant
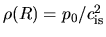 .
.
Figure 4.2 (left) shows three models of density distribution,
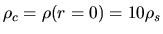 ,
,
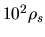 , and
, and 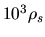 .
Comparing these three models,
it should be noticed that the cloud size (radius) decreases
with increasing the central density
.
Comparing these three models,
it should be noticed that the cloud size (radius) decreases
with increasing the central density 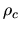 .
The mass of the cloud is obtained by integrating the distribution, which is illustrated against the
central-to-surface density ratio
.
The mass of the cloud is obtained by integrating the distribution, which is illustrated against the
central-to-surface density ratio 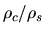 in Figure 4.2 (right).
The
in Figure 4.2 (right).
The 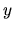 -axis represents a normalized mass as
-axis represents a normalized mass as
![$m=M/[4\pi \rho_s (c_{\rm is}/\sqrt{4\pi G \rho_s})^3]$](img869.png) .
The maximum value of
.
The maximum value of 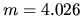 means
means
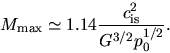 |
(4.9) |
This is the maximum mass which is supported against the self-gravity by the thermal pressure with an
isothermal sound speed of 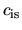 , when the cloud is immersed in the pressure
, when the cloud is immersed in the pressure 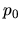 .
This is called Bonnor-Ebert mass [Bonnor (1956), Ebert (1955)].
It is to be noticed that the critical state
.
This is called Bonnor-Ebert mass [Bonnor (1956), Ebert (1955)].
It is to be noticed that the critical state
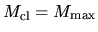 is achieved when the density contrast
is rather low
is achieved when the density contrast
is rather low
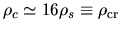 .
.
Another important result from Figure 4.2 (right) is the stability of an isothermal cloud.
Even for a cloud with
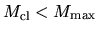 ,
any clouds on the part of
,
any clouds on the part of
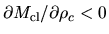 are unstable, whose clouds are distributed on the branch
with
are unstable, whose clouds are distributed on the branch
with
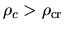 .
This is understood as follows:
For a hydrostatic cloud the mass should be expressed with the external pressure and
the central density [Fig.4.2 (right)] as
.
This is understood as follows:
For a hydrostatic cloud the mass should be expressed with the external pressure and
the central density [Fig.4.2 (right)] as
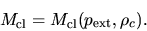 |
(4.10) |
In this case, a relation between the partial derivatives such as
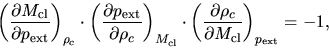 |
(4.11) |
is satisfied, unless each term is equal to zero.
Figure 4.1 (left) shows that
the cloud mass 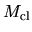 is a decreasing function of the external pressure
is a decreasing function of the external pressure
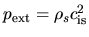 ,
if the central density is fixed.
Since this means
,
if the central density is fixed.
Since this means
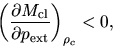 |
(4.12) |
equation (4.11) gives us
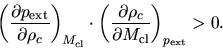 |
(4.13) |
For a cloud with
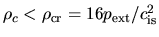 the mass is an increasing function of the central density as
the mass is an increasing function of the central density as
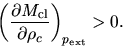 |
(4.14) |
Thus, equation (4.13) leads to the relation
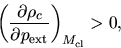 |
(4.15) |
for
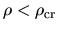 .
This means that gas cloud contracts (the central density and pressure increase),
when the external pressure increases.
This is an ordinary reaction of a stable gas.
.
This means that gas cloud contracts (the central density and pressure increase),
when the external pressure increases.
This is an ordinary reaction of a stable gas.
On the other hand, the cloud on the part of
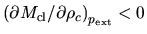 (for
(for
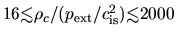 ) behaves
) behaves
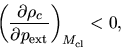 |
(4.16) |
and this represents that an extra external pressure decreases the central density and thus the pressure.
Pressure encourages expansion.
This reaction is unstable.
Figure 4.2:
(Left) radial density distribution.
Each curve has different 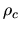 .
The x-axis denotes the radial distance normalized by a scale-length as
.
The x-axis denotes the radial distance normalized by a scale-length as
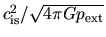 .
It is shown that the radius increases with decreasing
.
It is shown that the radius increases with decreasing 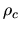 in this range
(
in this range
(
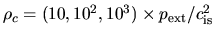 ).
(Right) The relation between mass (
).
(Right) The relation between mass (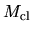 ) and the central density (
) and the central density (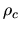 ) is plotted,
under the condition of constant external pressure.
The x-axis represents the central density normalized by
) is plotted,
under the condition of constant external pressure.
The x-axis represents the central density normalized by
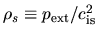 .
The y-axis represents the cloud mass normalized by
.
The y-axis represents the cloud mass normalized by
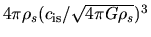 .
.
 |




Next: Equilibria of Cylindrical Cloud
Up: Hydrostatic Balance
Previous: Problem 2
Contents
Kohji Tomisaka
2007-07-08
![]() .
To establish a pressure equilibrium, the pressure at the surface
.
To establish a pressure equilibrium, the pressure at the surface
![]() must equal to
must equal to ![]() .
This means that the density at the surface is constant
.
This means that the density at the surface is constant
![]() .
.
![]() ,
,
![]() , and
, and ![]() .
Comparing these three models,
it should be noticed that the cloud size (radius) decreases
with increasing the central density
.
Comparing these three models,
it should be noticed that the cloud size (radius) decreases
with increasing the central density ![]() .
The mass of the cloud is obtained by integrating the distribution, which is illustrated against the
central-to-surface density ratio
.
The mass of the cloud is obtained by integrating the distribution, which is illustrated against the
central-to-surface density ratio ![]() in Figure 4.2 (right).
The
in Figure 4.2 (right).
The ![]() -axis represents a normalized mass as
-axis represents a normalized mass as
![]() .
The maximum value of
.
The maximum value of ![]() means
means
![]() ,
any clouds on the part of
,
any clouds on the part of
![]() are unstable, whose clouds are distributed on the branch
with
are unstable, whose clouds are distributed on the branch
with
![]() .
This is understood as follows:
For a hydrostatic cloud the mass should be expressed with the external pressure and
the central density [Fig.4.2 (right)] as
.
This is understood as follows:
For a hydrostatic cloud the mass should be expressed with the external pressure and
the central density [Fig.4.2 (right)] as
![]() (for
(for
![]() ) behaves
) behaves
