


Next: Ambipolar Diffusion
Up: Ambipolar Diffusion
Previous: Ambipolar Diffusion
Contents
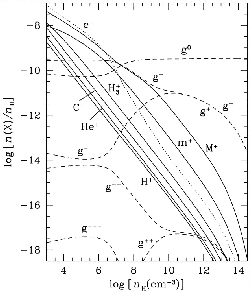
Figure 4.3:
Ionization fractions 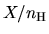 are plotted against the number density
are plotted against the number density
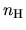 .
The ionization rate of an H
.
The ionization rate of an H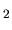 molecule by cosmic rays outside the cloud is
taken
molecule by cosmic rays outside the cloud is
taken
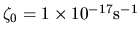 .
20% of C and O and 2% of metallic elements are assumed to
remain in the gas phase and the rest in grains.
.
20% of C and O and 2% of metallic elements are assumed to
remain in the gas phase and the rest in grains.
 |
In the dense clouds, the ionization fraction is low.
Since the uv/optical radiations from stars can not reach the cloud center,
potential ionization comes from the cosmic ray particles.
In this case the rate of ionization per volume is given as 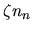 ,
where
,
where
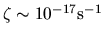 .
In Figure 4.3, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
.
In Figure 4.3, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
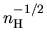 for
for
 .
This is understood as follows:
Equilibrium balance between one kind of ion
.
This is understood as follows:
Equilibrium balance between one kind of ion 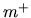 and its neutral
and its neutral 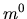
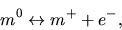 |
(4.35) |
is considered.
The recombination (reaction from the right to left) rate per unit volume
is expressed
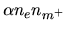 , while the ionization rate (left to right) per unit volume
is
, while the ionization rate (left to right) per unit volume
is 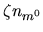 ,
where
,
where 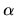 means the recombination rate coefficient.
Nakano (1984) obtained in the range of
means the recombination rate coefficient.
Nakano (1984) obtained in the range of
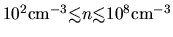
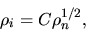 |
(4.36) |
where the numerical factor
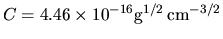 .
.



Next: Ambipolar Diffusion
Up: Ambipolar Diffusion
Previous: Ambipolar Diffusion
Contents
Kohji Tomisaka
2007-07-08


![]() ,
where
,
where
![]() .
In Figure 4.3, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
.
In Figure 4.3, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
![]() for
for
![]() .
This is understood as follows:
Equilibrium balance between one kind of ion
.
This is understood as follows:
Equilibrium balance between one kind of ion ![]() and its neutral
and its neutral ![]()