


Next: Gravitational Instability of Thin
Up: Physical Background
Previous: Problem
Contents
Sound wave seems to be modified in the medium where the self-gravity is important.
Beside the continuity equation (2.35)
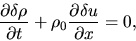 |
(2.45) |
and the equation of motion (2.37)
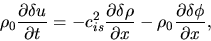 |
(2.46) |
the linearized Poisson equation
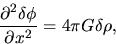 |
(2.47) |
should be included.
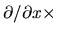 (2.46) gives
(2.46) gives
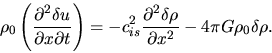 |
(2.48) |
where we used equation (2.47) to eliminate 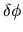 .
This yields
.
This yields
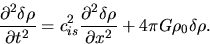 |
(2.49) |
where we used
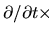 (2.45).
(2.45).
This is the equation which characterizes the growth of density perturbation owing to the self-gravity.
Here we consider the perturbation are expressed by the linear combination of plane waves as
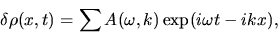 |
(2.50) |
where 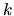 and
and 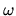 represent the wavenumber and the angular frequency of the wave.
Picking up a plane wave and putting into equation (2.49), we obtain the dispersion relation
for the gravitational instability as
represent the wavenumber and the angular frequency of the wave.
Picking up a plane wave and putting into equation (2.49), we obtain the dispersion relation
for the gravitational instability as
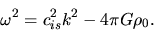 |
(2.51) |
Reducing the density to zero, the equation gives us the same dispersion relation as that of the sound wave as
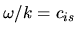 .
For short waves (
.
For short waves (
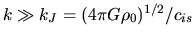 ), since
), since 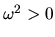 the wave is ordinary oscillatory wave.
Increasing the wavelength (decreasing the wavenumber),
the wave is ordinary oscillatory wave.
Increasing the wavelength (decreasing the wavenumber), 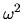 becomes negative for
becomes negative for
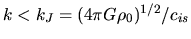 .
For negative
.
For negative 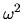 ,
, 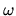 can be written
can be written
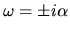 using a positive real
using a positive real 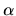 .
In this case, since
.
In this case, since
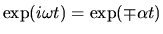 , the wave which has
, the wave which has
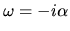 increases
its amplitude exponentially.
This means that even if there are density inhomogeneities only with small amplitudes,
they grow in a time scale of
increases
its amplitude exponentially.
This means that even if there are density inhomogeneities only with small amplitudes,
they grow in a time scale of 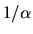 and form density inhomogeneities with large amplitudes.
and form density inhomogeneities with large amplitudes.
Figure 2.2:
Dispersion Relation
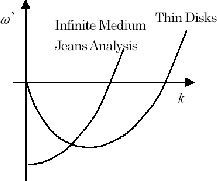 |
The critical wavenumber
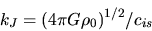 |
(2.52) |
corresponds to the wavelength
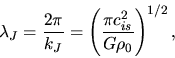 |
(2.53) |
which is called the Jeans wavelength.
Ignoring a numerical factor of the order of unity, it is shown that the Jeans wavelength is approximately equal to
the free-fall time scale (eq.[2.26]) times the sound speed.
The short wave with
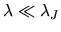 does not suffer from the self-gravity.
For such a scale, the analysis we did in the preceding section is valid.
does not suffer from the self-gravity.
For such a scale, the analysis we did in the preceding section is valid.
Typical values in molecular clouds,
such as
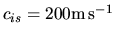 ,
,
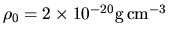 , give us the Jeans wavelength as
, give us the Jeans wavelength as
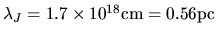 .
The mass contained in a sphere with a radius
.
The mass contained in a sphere with a radius 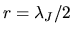 is often called Jeans mass,
which gives a typical mass scale above which the gas collapses.
Typical value of the Jeans mass is as follows
is often called Jeans mass,
which gives a typical mass scale above which the gas collapses.
Typical value of the Jeans mass is as follows
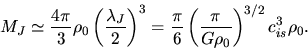 |
(2.54) |
Using again the above typical values in the molecular clouds,
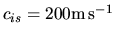 ,
,
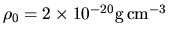 ,
the Jeans mass of this gas is equal to
,
the Jeans mass of this gas is equal to
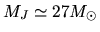 .
.



Next: Gravitational Instability of Thin
Up: Physical Background
Previous: Problem
Contents
Kohji Tomisaka
2007-11-02
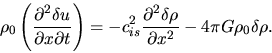
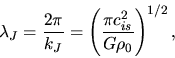
![]() ,
,
![]() , give us the Jeans wavelength as
, give us the Jeans wavelength as
![]() .
The mass contained in a sphere with a radius
.
The mass contained in a sphere with a radius ![]() is often called Jeans mass,
which gives a typical mass scale above which the gas collapses.
Typical value of the Jeans mass is as follows
is often called Jeans mass,
which gives a typical mass scale above which the gas collapses.
Typical value of the Jeans mass is as follows