


Next: Virial Analysis
Up: Hydrostatic Balance
Previous: Bonnor-Ebert Mass
Contents
In Figure 4.1 (right) we plotted the structure for a polytropic cloud.
Inner structure is not dependent of 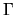 , it is clear the slope of the outer envelope
is dependent on
, it is clear the slope of the outer envelope
is dependent on 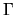 .
.
- In the case of the spherically symmetric, consider a polytrope (
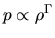 ) with
) with 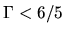 (at least the envelope of
(at least the envelope of
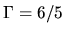 cloud extends to
cloud extends to 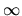 .),
in which gas extends to
.),
in which gas extends to 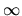 .
if
.
if
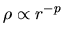 , the mass inside of
, the mass inside of 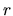 is proportional to
is proportional to
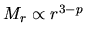 .
Thus, the gravity per unit volume at a radius
.
Thus, the gravity per unit volume at a radius 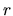 ,
, 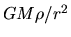 , is proportional to
, is proportional to
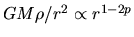 .
On the other hand the pressure force is
.
On the other hand the pressure force is
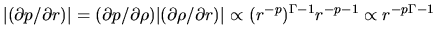 .
These two powers become the same, only if
.
These two powers become the same, only if
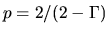 .
.
- In the case of cylindrical cloud with
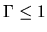 ,
the mass per unit length
,
the mass per unit length
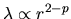 .
The gravity at
.
The gravity at 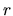 ,
,
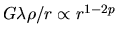 .
Note that the power is the same as the spherical case.
Since the power of the pressure force should be the same as the spherical case, the resultant
.
Note that the power is the same as the spherical case.
Since the power of the pressure force should be the same as the spherical case, the resultant 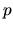 should be the same
should be the same
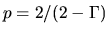 .
.
The case of 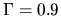 , an envelope extending to a large radius indicates the power-law distribution
much shallower than that of the isothermal
, an envelope extending to a large radius indicates the power-law distribution
much shallower than that of the isothermal 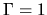 one.
one.



Next: Virial Analysis
Up: Hydrostatic Balance
Previous: Bonnor-Ebert Mass
Contents
Kohji Tomisaka
2007-11-02
![]() , it is clear the slope of the outer envelope
is dependent on
, it is clear the slope of the outer envelope
is dependent on ![]() .
.