Free-fall Time
Even if the pressure force can be neglected in the equation of motion
(A.1), the gravitational force remains.
Assuming the spherical symmetry, consider the gravity 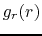 at the position
of radial distance from the center being equal to
at the position
of radial distance from the center being equal to 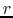 .
Using the Gauss' theorem,
.
Using the Gauss' theorem, 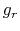 is related to the mass inside of
is related to the mass inside of 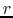 ,
which is expressed by the equation
,
which is expressed by the equation
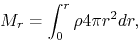 |
(2.12) |
and 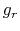 is written as
is written as
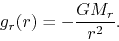 |
(2.13) |
This leads to the equation motion for a cold gas under a control of
the self-gravity is written
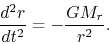 |
(2.14) |
Analyzing the equation is straightforward, multiplying 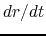 gives
gives
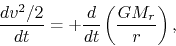 |
(2.15) |
which leads to the conservation of mechanical energy as
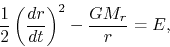 |
(2.16) |
in which 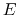 represents the total energy of the pressureless
gas element and it is obtained from the initial condition.
If the gas is static initially at the distance
represents the total energy of the pressureless
gas element and it is obtained from the initial condition.
If the gas is static initially at the distance 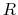 , the total
energy is negative as
, the total
energy is negative as
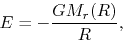 |
(2.17) |
because at 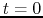 ,
, 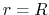 and
and 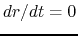 .
.
The solutions of equation (2.16) are well known as follows:
- the case of negative energy
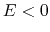 .
Considering the case that the gas sphere is inflowing
.
Considering the case that the gas sphere is inflowing 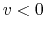 ,
equation (2.16) becomes
,
equation (2.16) becomes
![\begin{displaymath}
\frac{d r}{d t}=-\left[2GM_r(R)\right]^{1/2}\left(\frac{1}{r}-\frac{1}{R}\right)^{1/2},
\end{displaymath}](img405.png) |
(2.18) |
where we assumed initially 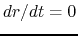 at
at 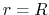 .
Using a parameter
.
Using a parameter 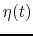 , the radius of the gas element
at some epoch
, the radius of the gas element
at some epoch 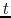 is written
is written
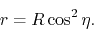 |
(2.19) |
In this case, equation (2.18) reduces to
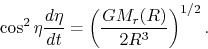 |
(2.20) |
This gives us the expression of 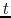 as
as
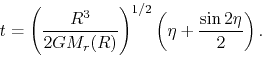 |
(2.21) |
This corresponds to the closed universe in the cosmic expansion
( ).
).
- if the energy is equal to zero,
the solution of equation (2.16) is written as
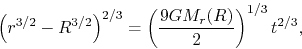 |
(2.22) |
where 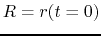 .
.
Subsections
Kohji Tomisaka
2009-12-10