Equation (2.26) indicates that the gas shell with a large 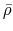 reaches
the center earlier than that with a small
reaches
the center earlier than that with a small 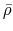 .
Imediately, this means a spherical cloud with a uniform density
.
Imediately, this means a spherical cloud with a uniform density 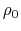 contracts
uniformly and all the mass reaches the center at
contracts
uniformly and all the mass reaches the center at
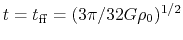 .
In this case, the mass accretion rate to a central source becomes infinity
at an epoch
.
In this case, the mass accretion rate to a central source becomes infinity
at an epoch 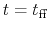 .
In contrast, consider a cloud whose density gradually decreases outwardly.
In this case, the outer mass shell has smaller
.
In contrast, consider a cloud whose density gradually decreases outwardly.
In this case, the outer mass shell has smaller 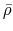 than the inner mass shell.
Therefore even when the inner mass shell collapses and reaches the center,
the outer mass shell are contracting and does not reach the center.
This gives a smaller mass accretion rate than a uniform cloud.
If the gas pressure is neglected, the accretion rate is determined by the initial spatial distribution
of the density.
We will compare the accretion rate derived here with results of hydrodynamical calculation
in
than the inner mass shell.
Therefore even when the inner mass shell collapses and reaches the center,
the outer mass shell are contracting and does not reach the center.
This gives a smaller mass accretion rate than a uniform cloud.
If the gas pressure is neglected, the accretion rate is determined by the initial spatial distribution
of the density.
We will compare the accretion rate derived here with results of hydrodynamical calculation
in  4.7
4.7
Kohji Tomisaka
2009-12-10