Convective Instability
Figure 2.4:
Convection.
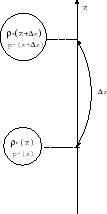 |
If water is heated from the bottom and temperature difference between the top
and the bottom exceeds a limit, convection is driven.
Water heated from the bottom climbes and cool water on the top descends.
This transfers the thermal energy from the bottom to the top.
In this section, we describe the condition in which convection is driven.
Consider a hydrostatic balanced atmosphere in which the hydrostatic
balance equation is satisfied:
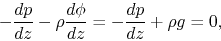 |
(2.78) |
where we assumed
 in equation (2.2)
and the gravity is working downwards in
in equation (2.2)
and the gravity is working downwards in  -direction (
-direction (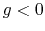 )
The pressure and density of the atmosphere are
)
The pressure and density of the atmosphere are 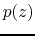 and
and 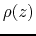 .
We consider a gas element (hatched region in Fig.2.4),
whose density
.
We consider a gas element (hatched region in Fig.2.4),
whose density 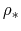 and
and 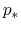 are equal to those of the
atmosphere
are equal to those of the
atmosphere 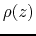 and
and 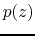 as
as
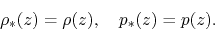 |
(2.79) |
Further, we assume this gas element to move from 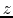 to
to 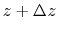 adiabatically, that is,
adiabatically, that is,
![\begin{displaymath}
\frac{p_*(z+\Delta z)}{\left[\rho_*(z+\Delta z)\right]^\gamma}
=\frac{p_*(z)}{\left[\rho_*(z)\right]^\gamma}.
\end{displaymath}](img550.png) |
(2.80) |
Pressure balance is required between the pressures of the gas element
at 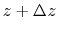 ,
,
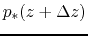 ,
and the atmosphere
,
and the atmosphere 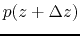 .
If the density of the gas element at
.
If the density of the gas element at 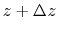 ,
,
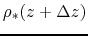 ,
is smaller than that of the atmosphere,
the gravity force in equation (2.78) is weaker than
the pressure force and the element keeps climbing.
Thus the condition for the convective instability is written as
,
is smaller than that of the atmosphere,
the gravity force in equation (2.78) is weaker than
the pressure force and the element keeps climbing.
Thus the condition for the convective instability is written as
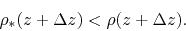 |
(2.81) |
Using
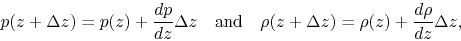 |
(2.82) |
we can rewrite equation (2.81) into
the relation in the variables of the atmosphere (variables without *) as
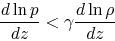 |
(2.83) |
or
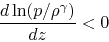 |
(2.84) |
This means the specific entropy
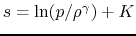 decreases upwardly. Thus, if we consider the adiabatic process, the atmosphere
in which a specific entropy decreases upwardly is unstable for the convection.
decreases upwardly. Thus, if we consider the adiabatic process, the atmosphere
in which a specific entropy decreases upwardly is unstable for the convection.
Problem
Obtain equation (2.83) from equation
(2.81) using equation
(2.82).
Kohji Tomisaka
2009-12-10