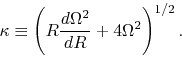In the case of a rotating disk with an angular rotation speed 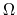 ,
basic equations are
,
basic equations are
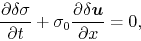 |
(2.66) |
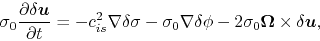 |
(2.67) |
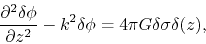 |
(2.68) |
where the third term of r.h.s. of
equation (2.67)
represents the Colioris force.
Equation (2.68) gives
a solution identical to equation (2.64) as
![\begin{displaymath}
\delta \phi=-\frac{2\pi G \delta \sigma}{k}
\exp\left[i(\omega t-kx)-k\vert z\vert\right].
\end{displaymath}](img527.png) |
(2.69) |
Choosing a direction in which the wavenumber vector can be expressed as
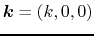 ,
we can reduce equations (2.66)
and (2.67) to
,
we can reduce equations (2.66)
and (2.67) to
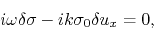 |
(2.70) |
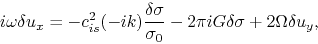 |
(2.71) |
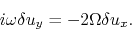 |
(2.72) |
These three equations together with equation (2.69)
bring us a dispersion relation as
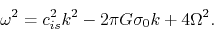 |
(2.73) |
Comparing with equation(2.65),
this indicates rotation works to stabilize the system.
Equation (2.73) is rewritten as
![\begin{displaymath}
\omega^2=c_{is}^2\left(k-\frac{\pi G \sigma_0}{c_{is}^2}\rig...
...
\left[\frac{4\Omega^2c_{is}^2}{(\pi G \sigma_0)^2}-1\right].
\end{displaymath}](img533.png) |
(2.74) |
Defining
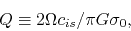 |
(2.75) |
we can see that
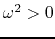 for all wavenumbers if
for all wavenumbers if 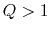 and
that if
and
that if 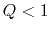 for some range of wavenumber
for some range of wavenumber 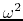 becomes negative.
A rotating disk with
becomes negative.
A rotating disk with 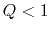 is unstable for some range of wavenumber.
This number is called Toomre's
is unstable for some range of wavenumber.
This number is called Toomre's 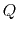 .
This is useful to see whether a galactic disk is stable or not.
For the galactic disk, Toomre's
.
This is useful to see whether a galactic disk is stable or not.
For the galactic disk, Toomre's 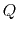 must be modified as
must be modified as
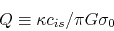 |
(2.76) |
where 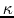 represents the epicyclic frequency as
represents the epicyclic frequency as
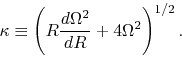 |
(2.77) |
See section 3.5 for the galactic disk.
Kohji Tomisaka
2009-12-10
![\begin{displaymath}
\omega^2=c_{is}^2\left(k-\frac{\pi G \sigma_0}{c_{is}^2}\rig...
...
\left[\frac{4\Omega^2c_{is}^2}{(\pi G \sigma_0)^2}-1\right].
\end{displaymath}](img533.png)