Virial Analysis
For a system to achive a mechanical equlibrium,
a relation must be satisfied
between energies such as potential, thermal and kinetic energies.
This is called the Virial relation.
For example, a harmonic oscillator
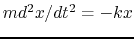 has
a potetial energy of
has
a potetial energy of
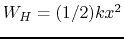 and a kinetic energy
and a kinetic energy
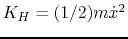 .
Averaging these two energies over one period,
both energies give the same absolute value proportional to the oscillation
amplitude
.
Averaging these two energies over one period,
both energies give the same absolute value proportional to the oscillation
amplitude 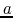 squared as
squared as
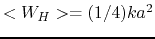 and
and
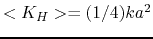 .
Another example is a Kepler problem.
For simplicity, consider mass
.
Another example is a Kepler problem.
For simplicity, consider mass 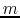 running
on a circular orbit with a radius
running
on a circular orbit with a radius 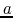 from a body with a mass
from a body with a mass 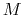 .
The gravitational and kinetic energies are equal to
.
The gravitational and kinetic energies are equal to 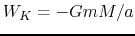 and
and
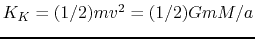 , where we used the centrifugal balance
as
, where we used the centrifugal balance
as
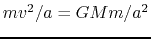 .
As a result,
for the harmonic oscillator
.
As a result,
for the harmonic oscillator
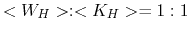 while for the circular
Kepler problem
while for the circular
Kepler problem 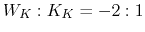 .
This ratio is known to be related to the power
.
This ratio is known to be related to the power 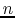 of
the potetial as
of
the potetial as
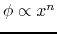 .
Important nature of the self-gravity is understood only with this relation
without solving the hydrostatic balance equations.
In the following, we describe the Virial relation satisfied with isolated
systems such as stars.
.
Important nature of the self-gravity is understood only with this relation
without solving the hydrostatic balance equations.
In the following, we describe the Virial relation satisfied with isolated
systems such as stars.
Hydrodynamic equation of motion using the Lagrangean time derivative [eq.(A.3)] is
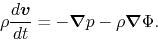 |
(2.104) |
For simplicity, consider a spherical symmetric configuration.
The equation of motion is expressed as
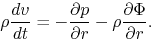 |
(2.105) |
Multiplying radius 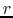 to the equation
and integrating by the volume
to the equation
and integrating by the volume 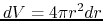 over a volume
from
over a volume
from 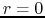 to
to 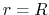 , we obtain the Virial relation as
, we obtain the Virial relation as
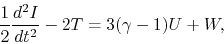 |
(2.106) |
where
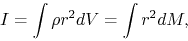 |
(2.107) |
is an inertia of this body,
and 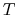 and
and 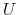 are, respectively, the kinetic and thermal energies as
are, respectively, the kinetic and thermal energies as
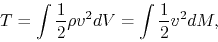 |
(2.108) |
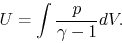 |
(2.109) |
Further,
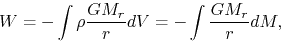 |
(2.110) |
is a gravitational energy, where
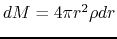 and
and
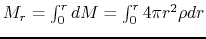
Since
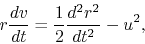 |
(2.111) |
the lefthand-side of equation (2.105) is rewritten as
using equations (2.107) and (2.108).
On the other hand, the first term of the rhs of equation (2.105)
becomes
To derive this equation, we have assumed the pressure diminishes
at a radius 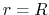 and the surface pressure term does not appear in the
final expression.
This is valid for an isolated system such as a star.
and the surface pressure term does not appear in the
final expression.
This is valid for an isolated system such as a star.
The last term of the rhs of equation (2.105) is written as
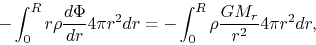 |
(2.114) |
wher we used equation (2.13).
This is rewritten as
The energy 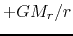 per unit mass is necessary for a gas element
to move from the radius
per unit mass is necessary for a gas element
to move from the radius 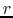 , inside which mass
, inside which mass 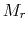 is contained, to the
infinity.
Adding the energy
is contained, to the
infinity.
Adding the energy 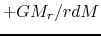 for all the gas,
the potential energy is obtained.
In the case of a star composed of uniform density
for all the gas,
the potential energy is obtained.
In the case of a star composed of uniform density 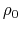 ,
,
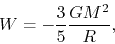 |
(2.116) |
where
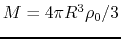 .
.
To obtain a condition for the mechanical equilibrium, we assume 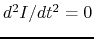 .
Equation (2.106) becomes
.
Equation (2.106) becomes
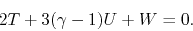 |
(2.117) |
Assuming the stystem is static 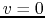 , the above equation reduces to
, the above equation reduces to
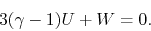 |
(2.118) |
In the case of 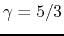 this reduces to
this reduces to 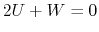 .
The total energy
.
The total energy 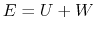 is expressed as
is expressed as
For the gas with 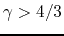 , equation (2.119) gives
a negative total energy
, equation (2.119) gives
a negative total energy 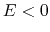 and the system is in a confined state.
However, if
and the system is in a confined state.
However, if 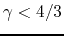 , the gravity can not confine the gas.
, the gravity can not confine the gas.
For
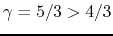 , equation (2.118) gives
, equation (2.118) gives
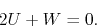 |
(2.120) |
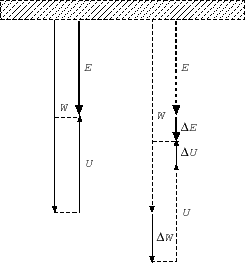
This shows us a strange nature of the self-gravitating gas (see Fig. 2.10).
That is, if the heat flux flows outward, the total energy decreases
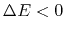 .
The system must contract and equation (2.119)
indicates
.
The system must contract and equation (2.119)
indicates
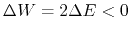 (the gravitational energy decreases:
the absolute value of the gravitational energy increases).
However, for the thermal energy,
equation (2.120) indicates that
(the gravitational energy decreases:
the absolute value of the gravitational energy increases).
However, for the thermal energy,
equation (2.120) indicates that
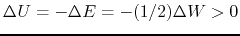 for this system to be static.
This shows that if the heat flux flows out from the system
the thermal energy increases in the self-gravitating system.
This comes from the contraction due to the gravity.
for this system to be static.
This shows that if the heat flux flows out from the system
the thermal energy increases in the self-gravitating system.
This comes from the contraction due to the gravity.
Figure 2.10:
Virial relation for stars composed of 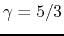 gas.
gas.
 |
Kohji Tomisaka
2009-12-10
![]() has
a potetial energy of
has
a potetial energy of
![]() and a kinetic energy
and a kinetic energy
![]() .
Averaging these two energies over one period,
both energies give the same absolute value proportional to the oscillation
amplitude
.
Averaging these two energies over one period,
both energies give the same absolute value proportional to the oscillation
amplitude ![]() squared as
squared as
![]() and
and
![]() .
Another example is a Kepler problem.
For simplicity, consider mass
.
Another example is a Kepler problem.
For simplicity, consider mass ![]() running
on a circular orbit with a radius
running
on a circular orbit with a radius ![]() from a body with a mass
from a body with a mass ![]() .
The gravitational and kinetic energies are equal to
.
The gravitational and kinetic energies are equal to ![]() and
and
![]() , where we used the centrifugal balance
as
, where we used the centrifugal balance
as
![]() .
As a result,
for the harmonic oscillator
.
As a result,
for the harmonic oscillator
![]() while for the circular
Kepler problem
while for the circular
Kepler problem ![]() .
This ratio is known to be related to the power
.
This ratio is known to be related to the power ![]() of
the potetial as
of
the potetial as
![]() .
Important nature of the self-gravity is understood only with this relation
without solving the hydrostatic balance equations.
In the following, we describe the Virial relation satisfied with isolated
systems such as stars.
.
Important nature of the self-gravity is understood only with this relation
without solving the hydrostatic balance equations.
In the following, we describe the Virial relation satisfied with isolated
systems such as stars.
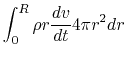
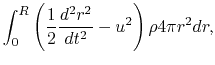
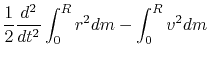
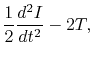
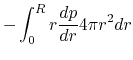
![$\displaystyle -\left\{\left[4\pi r^3 p\right]_0^R -3\int_0^R 4\pi r^2 p dr \right\},$](img647.png)
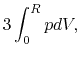
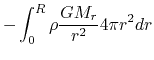
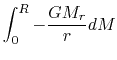
![]() .
Equation (2.106) becomes
.
Equation (2.106) becomes
![]() , equation (2.118) gives
, equation (2.118) gives