Consider the case of 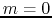 axisymmetric perturbations.
Equation (3.32) becomes
axisymmetric perturbations.
Equation (3.32) becomes
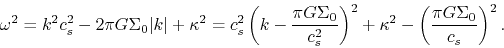 |
(3.33) |
If 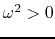 the system is stable against the axisymmetric perturbation, while
if
the system is stable against the axisymmetric perturbation, while
if 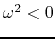 the system is unstable.
Defining
the system is unstable.
Defining
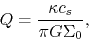 |
(3.34) |
if 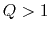 ,
, 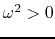 for all wavenumbers
for all wavenumbers 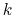 .
On the other hand, if
.
On the other hand, if 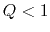 ,
, 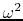 becomes negative for some wavenumbers
becomes negative for some wavenumbers 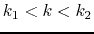 .
Therefore, the Toomre's
.
Therefore, the Toomre's 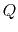 number gives us a criterion whether the system is unstable or not
for the axisymmetric perturbation.
[Recommendation for a reference book of this section: Binney & Tremaine (1988).]
number gives us a criterion whether the system is unstable or not
for the axisymmetric perturbation.
[Recommendation for a reference book of this section: Binney & Tremaine (1988).]
The condition is expressed as
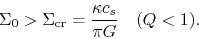 |
(3.35) |
Kennicutt plotted
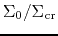 against the normalized radius as
against the normalized radius as 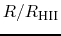 for various
galaxies, where
for various
galaxies, where 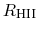 represents the maximum distance of HII regions from the center
(Fig.3.8).
Since
represents the maximum distance of HII regions from the center
(Fig.3.8).
Since
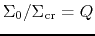 , Figure 3.8 shows that HII regions are observed mainly in
the region with
, Figure 3.8 shows that HII regions are observed mainly in
the region with 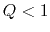 but those are seldom seen in the outer low-density
but those are seldom seen in the outer low-density 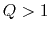 region.
This seems the gravitational instability plays an important role.
region.
This seems the gravitational instability plays an important role.
Figure 3.8:
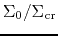 vs
vs 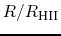 .
.
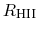 represents the maximum distance of HII regions from the center.
The sound speed is assumed constant
represents the maximum distance of HII regions from the center.
The sound speed is assumed constant
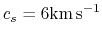 .
Taken from Fig.11 of
Kennicutt (1989).
.
Taken from Fig.11 of
Kennicutt (1989).
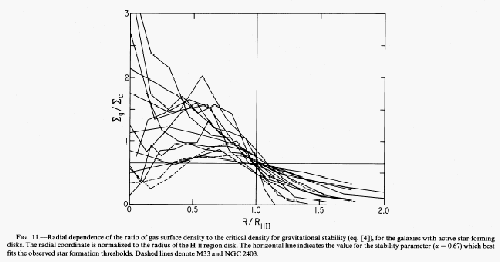 |
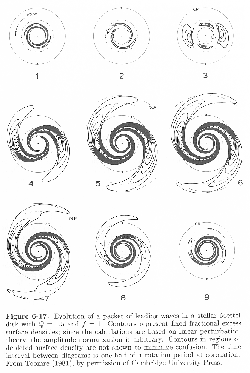
Figure:
Numerical simulation of the swing amplification mechanism.
The number attached each panel shows the time sequence.
This is obtained by the time-dependent linear analysis.
First, perturbation with leading spiral pattern is added to the Mestel disk with 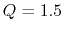 .
The leading spiral gradually unwinds and become a trailing spiral.
Loosely wound spiral pattern winds gradually and the last panel shows a tightly wound leading spiral pattern.
The final amplitude is
.
The leading spiral gradually unwinds and become a trailing spiral.
Loosely wound spiral pattern winds gradually and the last panel shows a tightly wound leading spiral pattern.
The final amplitude is 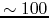 times larger than that of the initial state.
times larger than that of the initial state.
 |
The above discussion is for the gaseous disk.
The Toomre's 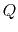 value is also defined for stellar system as
value is also defined for stellar system as
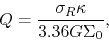 |
(3.36) |
where 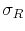 represents the radial velocity dispersion.
represents the radial velocity dispersion.
For non-axisymmetric waves, even if
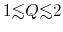 the instability grows.
To explain this, the swing amplification mechanism is proposed (Toomre 1981).
If there is a leading spiral perturbation in the disk with
the instability grows.
To explain this, the swing amplification mechanism is proposed (Toomre 1981).
If there is a leading spiral perturbation in the disk with
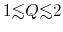 ,
the wave unwinds and finally becomes a trailing spiral pattern.
At the same time, the amplitude of the wave (perturbations) is amplified (see Fig.3.9).
,
the wave unwinds and finally becomes a trailing spiral pattern.
At the same time, the amplitude of the wave (perturbations) is amplified (see Fig.3.9).
Kohji Tomisaka
2009-12-10
![]() axisymmetric perturbations.
Equation (3.32) becomes
axisymmetric perturbations.
Equation (3.32) becomes


![]() value is also defined for stellar system as
value is also defined for stellar system as
![]() the instability grows.
To explain this, the swing amplification mechanism is proposed (Toomre 1981).
If there is a leading spiral perturbation in the disk with
the instability grows.
To explain this, the swing amplification mechanism is proposed (Toomre 1981).
If there is a leading spiral perturbation in the disk with
![]() ,
the wave unwinds and finally becomes a trailing spiral pattern.
At the same time, the amplitude of the wave (perturbations) is amplified (see Fig.3.9).
,
the wave unwinds and finally becomes a trailing spiral pattern.
At the same time, the amplitude of the wave (perturbations) is amplified (see Fig.3.9).