Next: Tightly Wound Spirals Up: Galactic Scale Star Formation Previous: Distributions of Atomic and Contents
Here, we will derive the dispersion relation for the gravitational instability of a rotating thin disk.
We will see the spatial variation of Toomre's ![]() parameter, which determines the stability of the rotating disk,
explains the nonlinearity of star formation rate, that is, there is a threshold density and no stars are formed in the
low density region.
parameter, which determines the stability of the rotating disk,
explains the nonlinearity of star formation rate, that is, there is a threshold density and no stars are formed in the
low density region.
Use the cylindrical coordinate ![]() and the basic equations for thin disk in
and the basic equations for thin disk in ![]() 2.6.
In linear analysis, we assume
2.6.
In linear analysis, we assume
![]() ,
,
![]() ,
,
![]() ,
where
,
where ![]() and
and ![]() represent the radial and azimuthal components of the velocity.
Linearized continuity equation is
represent the radial and azimuthal components of the velocity.
Linearized continuity equation is
Linearized equations of motion are
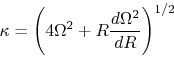 |
(3.12) |
We assume any solution of equations (3.9), (3.10) and(3.11) can be
written as a sum of terms of the form
| (3.18) |