Next: Ambipolar Diffusion Up: Ambipolar Diffusion Previous: Ambipolar Diffusion Contents
 |
In the dense clouds, the ionization fraction is low.
Since the uv/optical radiations from stars can not reach the cloud center,
potential ionization comes from the cosmic ray particles.
In this case the rate of ionization per volume is given as ![]() ,
where
,
where
![]() .
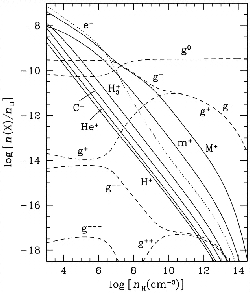
In Figure 4.6, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
.
In Figure 4.6, the ionization fraction for various density is shown
(Nakano, Nishi, & Umebayashi 2002).
This clearly shows that the fraction of ions decrease approximately in proportion to
![]() for
for
![]() .
This is understood as follows:
Equilibrium balance between one kind of ion
.
This is understood as follows:
Equilibrium balance between one kind of ion ![]() and its neutral
and its neutral ![]()
| (4.45) |
Kohji Tomisaka 2009-12-10