Figure 4.13:
Magneto-centrifugal wind model.
Figure shows the effective potential for a gas parcel with conserving the angular rotation speed
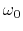 of the disk (eq.4.99).
The gas parcel is assumed to located originally at
of the disk (eq.4.99).
The gas parcel is assumed to located originally at 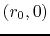 .
The
.
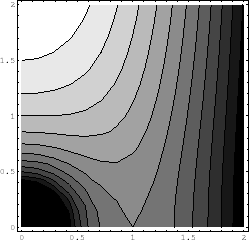
The 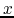 - and
- and 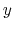 -axes mean normalized distance from the central star as
-axes mean normalized distance from the central star as  and
and 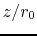 .
The darker color represents the deeper potential.
.
The darker color represents the deeper potential.
 |
To accelerate gas till supersonic speed, the magnetic force is considered to be an important player.
Blandford & Payne (1982) have proposed the ``magneto-centrifugal wind model'' for the acceleration in
two-dimensional axisymmetric configuration.
Figure 4.13 explains the magneto-centrifugal wind mechanism
(Fig. 1 of Blandford & Payne 1982).
Consider a disk under the gravity of a central star with mass 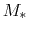 .
Assume that gas in the disk at the radius
.
Assume that gas in the disk at the radius 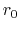 rotates with a Kepler speed of
rotates with a Kepler speed of
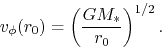 |
(4.98) |
Consider a gas parcel whose original position was 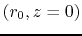 .
The effective potential for the particle rotating with an angular rotation speed of
.
The effective potential for the particle rotating with an angular rotation speed of
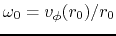 is written as
is written as
![\begin{displaymath}
\phi(r,z) =-\frac{GM_*}{\left(r^2+z^2\right)^{1/2}}-\frac{1}...
...right)^{1/2}}+\frac{1}{2}\left(\frac{r}{r_0}\right)^2\right],
\end{displaymath}](img1360.png) |
(4.99) |
where
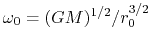 .
(Be careful that ordinary effective potential is calculated for constant angular momentum.
However, this is for constant angular rotation speed.)
The gas will co-rotate with the same angular rotation speed as the disk, if the magnetic field is
sufficiently strong.
Equation (4.99) corresponds the effective potential for the gas co-rotating
with the disk at
.
(Be careful that ordinary effective potential is calculated for constant angular momentum.
However, this is for constant angular rotation speed.)
The gas will co-rotate with the same angular rotation speed as the disk, if the magnetic field is
sufficiently strong.
Equation (4.99) corresponds the effective potential for the gas co-rotating
with the disk at 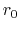 .
Figure 4.13 plots the isopotential contour lines for the effective potential
[eq.(4.99)].
The contour line passing the point
.
Figure 4.13 plots the isopotential contour lines for the effective potential
[eq.(4.99)].
The contour line passing the point 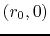 represents
represents
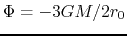 .
The angle between the isopotential line of
.
The angle between the isopotential line of
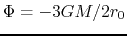 and the
and the 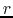 -axis is equal to
-axis is equal to 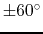 (see problem below).
Further, it can be obtained that the effective potential increases upwardly while
it decreases with reaching the central star or radially outwardly.
(see problem below).
Further, it can be obtained that the effective potential increases upwardly while
it decreases with reaching the central star or radially outwardly.
This leads to an important conclusion that
- If the angle between the magnetic field line and the
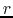 -axis
-axis
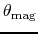 is larger than
is larger than
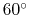 (
(
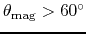 ), gas parcel moving along the field line must climb
the effective potential.
It needs extra energy to depart from the disk.
), gas parcel moving along the field line must climb
the effective potential.
It needs extra energy to depart from the disk.
- If
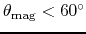 , gas parcel moving along the field line slides down
the effective potential.
It can depart from the disk without extra energy.
, gas parcel moving along the field line slides down
the effective potential.
It can depart from the disk without extra energy.
Be careful that this is valid if the magnetic field is sufficiently strong.
If the Kepler disk is threaded with the magnetic field lines with a shallow angle,
and if the angular momentum is sufficiently transferred along the magnetic field line,
in this case, the gas is accelerated by the extra centrifugal force
and finally escapes from the potential well of the central star.
This mechanism is called the ``magneto-centrifugal wind'' mechanism.
Subsections
Kohji Tomisaka
2009-12-10

![]() .
Assume that gas in the disk at the radius
.
Assume that gas in the disk at the radius ![]() rotates with a Kepler speed of
rotates with a Kepler speed of