In a diffuse cloud, the centrifugal force does not play an important role.
Consider a gas parcel whose specific angular momentum is equal to 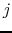 .
When the gas element contracts till the distance
.
When the gas element contracts till the distance 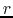 from the center,
the centrifugal force per mass of
from the center,
the centrifugal force per mass of
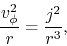 |
(4.101) |
works.
Contraction stops when the gravitational acceleration 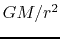 is balanced
by the centrifugal force.
Its radius (centrifugal radius) is expressed as
is balanced
by the centrifugal force.
Its radius (centrifugal radius) is expressed as
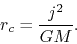 |
(4.102) |
Assuming that the disk is near the hydrostatic balance in 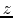 -direction,
total column density is related to the volume density on the
-direction,
total column density is related to the volume density on the 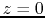 plane as
plane as
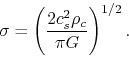 |
(4.103) |
We can show that a nondimensional ratio of specific angular momentum to the mass is equal to
the ratio of the free-fall time to the rotation period as follow:
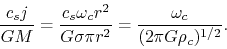 |
(4.104) |
Many numerical simulations confirm that
the contracting disk in the runaway isothermal contraction phase has some `universality.'
The ratio of the free-fall time to the rotation period is approximately equal to
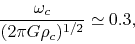 |
(4.105) |
regardless of the initial conditions (Matsumoto, Nakamura, & Hanawa 1997).
Thus,
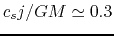 .
Finally, we can see the centrifugal radius as
.
Finally, we can see the centrifugal radius as
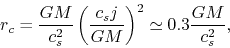 |
(4.106) |
increases with time in proportional to the mass 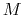 ,
because gas element with large
,
because gas element with large 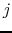 contracts later.
As the centrifugal radius increases with time, the launching point of the outflow
also expands with time.
contracts later.
As the centrifugal radius increases with time, the launching point of the outflow
also expands with time.
Kohji Tomisaka
2009-12-10
![]() .
When the gas element contracts till the distance
.
When the gas element contracts till the distance ![]() from the center,
the centrifugal force per mass of
from the center,
the centrifugal force per mass of
