Random Velocity
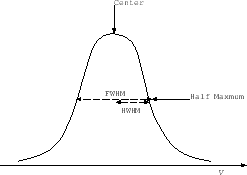
Figure E.1:
HWHM (half width of half maximum: the line width measured from the
the center of the emission line to the point of the half intensity)
and FWHM (full width of half maximum: the line width measured
between the points of the half intensity).
 |
Considering gas in Maxwellian velocity distribution,
the distribution function for the velocity is as follows:
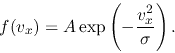 |
(E.1) |
This gives the one-dimensional random velocity as
If we observe emissions from such a gas,
the emission line is broaden due to the Doppler shift.
Using equation (E.2),
the HWHM (half width of half maximum: the line width measured from the
the center of the emission line to the point of the half intensity; see
Fig.E.1)
of the emission line is
![\begin{displaymath}
\exp\left[-\left(\frac{v_{x,\rm HWHM}}{2<v_x^2>}\right)^2 \right]=\frac{1}{2},
\end{displaymath}](img1768.png) |
(E.3) |
which leads to
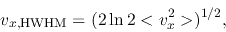 |
(E.4) |
and
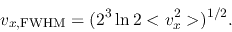 |
(E.5) |
Thus, if we assume isotropic distribution,
three-dimensional random velocity of gas
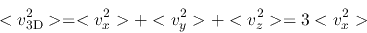 |
(E.6) |
is obtained with the line width as
Kohji Tomisaka
2012-10-03

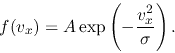
![\begin{displaymath}
\exp\left[-\left(\frac{v_{x,\rm HWHM}}{2<v_x^2>}\right)^2 \right]=\frac{1}{2},
\end{displaymath}](img1768.png)