Mass Spectrum

We have seen that a molecular cloud consists in many molecular cloud cores. For many years, there are attempts to determine the mass spectrum of the cores.

From a radio molecular line survey, a mass of each cloud core is determined. Plotting a histogram of number of cores against the mass, we have found that a mass spectrum can be fitted by a power law as

$$\frac{d N}{d M}=M^{n}$$ (1.18)

where $dN/dM$ represents the number of cores per unit mass interval. Many observation indicate that $n \sim -1.5$ as Table 1.1.

Table 1.1: Mass spectrum indicies derived with molecular line surveys.

Paper	$n$	Region	Observation	Mass range
Loren (1989)	$-1.1$	$\rho$ Oph		$10 M_\odot\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}... ...ox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 300 M_\odot$
Stutzki & Guesten (1990)	$-1.7\pm 0.15$	M17 SW	C$^{18}$O ($J=2-1$), S$^{34}$S ($J=2-1$, $J=3-2$)	${\rm a few }M_\odot\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.... ...3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} {\rm a few }10^3 M_\odot$
Lada et al. (1991)	$-1.6$	L1630	CS ($J=2-1$)	$M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 20M_\odot$
Nozawa et al. (1991)	$-1.7$	$\rho$ Oph North	$^{13}$CO ($J=1-0$)	$3M_\odot\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} ... ...ox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 160 M_\odot$
Tatematsu et al. (1993)	$-1.6 \pm 0.3$	Orion A	CS ($J=1-0$)	$M \mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 50 M_\odot$
Dobashi et al. (1996)	$-1.6$	Cygnus	$^{13}$CO ($J=1-0$)	$M \mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 100 M_\odot$
Onish et al (1996)	$-0.9\pm 0.2$	Taurus	C$^{18}$O ($J=1-0$)	$3 M_\odot \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}... ...box{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 80 M_\odot$
Motte, André, & Neri (1998)	$-1.5$	$\rho$Oph	$\lambda=1.3$mm	$M \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.5M_\odot$
	$-2.5$			$M \mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.5M_\odot$
Testi & Sargent (1998)	$-2.1$	Sarpens	$\lambda=3$mm	$1 M_\odot \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}... ...box{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 30 M_\odot$
Kramer et al.(1998)	$-1.6\sim -1.8$	L1457 etc$^*$	$^{12}$CO, $^{13}$CO, C$^{18}$O ($J=1-0$, $2-1$)	$10^{-4}M_\odot \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\... ...x{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10^4 M_\odot$
Heithausen et al. (1998)	$-1.84$	MCLD 123.5 + 24.9, Polaris Flare	$^{12}$CO($J=1-0$ and $2-1$)	$M_J \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} M \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10 M_\odot$
Johnstone et al. (2000)	$-2\sim -2.5$	$\rho$Oph	$\lambda=850\mu{\rm m}$	$M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.6M_\odot$
	$-1.5$			$M\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.6M_\odot$
Johnstone et al. (2001)	$-2.5\sim -3$	Ori B	$\lambda=850\mu{\rm m}$	$M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} M_\odot$
Onishi et al. (2002)	$-2.5$	Taurus	H$^{13}$CO$^+$ ($J=1-0$)	$3.5 M_\odot \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim... ...x{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 20.1 M_\odot$
Ikeda, Sunada, & Kitamura (2007)	$-2.3\pm 0.1$	Ori A	H$^{13}$CO$^+$ ($J=1-0$)	$M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 9 M_\odot$
	$-0.4\pm 0.1$			$M\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 9 M_\odot$
Ikeda & Kitamura (2009)	$-2.3\pm 0.3$	Ori A	C$^{18}$O ($J=1-0$)	$M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 5 M_\odot$

$^*$ MCLD126.6+24.5, NGC 1499 SW, Orion B South, S140, M17 SW, and NGC 7538

Figure 1.31: Cumulative mass distribution of the 70 pre-stellar condensations of NGC 2068/2071. The dotted and dashed lines are power-laws corresponding to the mass spectrum of CO clumps (Kramer et al. 1996) and to the IMF of Salpeter (1955), respectively. Taken from Fig.3 of Motte et al (2001).

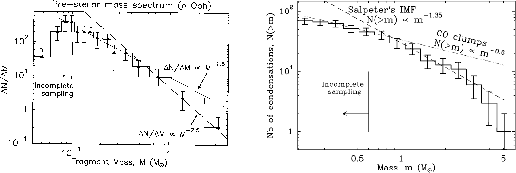Figure 1.31(left) (André, Ward-Thomson, & Barsony 2000) shows a mass spectrum function $dN/dM$ for 59 $\rho$ Oph cloud prestellar cores obtained at the IRAM 30-m telescope with the MPIfR 19-channel bolometer array. Presetellar cores with a mass $\sim M_\odot$ has a spectrum of $dN/dM\propto M^{-2.5}$ ($n=-2.5$) for $M \mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.5M_\odot$. While the right panel (Motte et al 2001) shows the cumulative mass spectrum ($N(>M)$ vs. $M$) of the 70 starless condensations identified in NGC 2068/2071. The mass spectrum for the 30 condensations of the NGC 2068 sub-region is very similar in shape. The best-fit power-law is $N(>M)\propto M^{n+1}\propto M^{-1.1}$ above $M\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 0.8M_\odot$. That is, $n=-2.1$. This power derived from the dust thermal emission is different from that derived by the radio molecular emission lines. Table 1.1 summarizes the observations to calculate the power index of core mass function.

The mass fuction of newborn stars is called as initial mass fuction (IMF). IMF for field stars in the solar neighborhood has been obtained as shown in Figure 1.33. The most famous one is Salpeter's IMF as $dN_*/dM_*\propto M_*^{-2.35}$ (Salpeter 1955). The low-mass end is flatter than that of $M_*\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} M_\odot$ as $dN_*/dM_*\propto M*^{-1.2}$ for $0.1M_\odot\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}... ...\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 1M_\odot$ while $dN_*/dM_*\propto M*^{-2.7}$ for $1M_\odot\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} ... ...mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10M_\odot$ (Meyer et al. 2000). The powers of stellar ( $-2.7 \sim -2.35$) and prestellar ($-2.5\sim -2.1$) mass functions are similar. If one prestellar core forms one star, the stellar mass $M_*$ is proportional to the prestellar core mass as $M_*=fM_{\rm core}$ and $f\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 1$, the mass spectrum of prestellar cores completely determines the IMF.

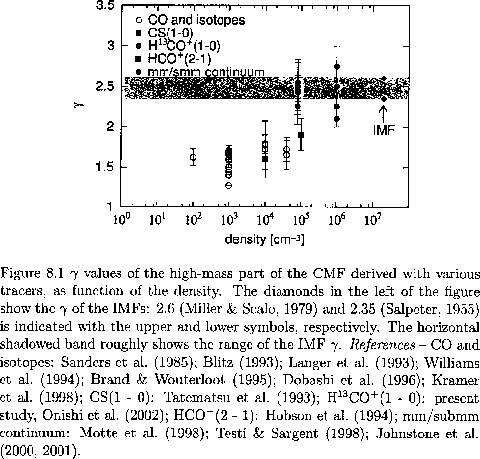
Figure 1.32 plots the power-law indices against the typical gas densities of respective observations, in which the critical density is taken as a typical density for molecular line studies. The power-law index is an increasing function of the typical gas densitiy $n_{\rm gas}$ (Ikeda 2007) and the cores with $n_{\rm gas}\mbox{\raisebox{0.3ex}{$>$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10^5{\rm cm}^{-3}$ have the same power-law index as the IMF. This may indicates these cores are the sites of star formation or direct parents of new-born stars^1.1.

Figure 1.32: The power-law index of $n=\gamma$ of core mass function $dN(M)/dM\propto M^{-n}$. $n$ is plotted against typical densities of observed molecular cores. In molecular line observations, the typical densities are assumed equal to the critical densities of the transitions of respective molecular line observations. For mm and sub-mm dust emission, the density is assumed $\sim 10^6{\rm cm}^{-3}$. Taken from Fig.8.1 of PhD Thesis of Ikeda (2007).

Figure 1.33: Comparison of initial mass fuctions for field stars in the solar neighbourhood. Respective symbols represent S55: Salpeter (1955), MS: Miller & Scalo (1979), Scalo 86: Scalo (1986) and KTG93: Kroupa, Tout, & Gilmore 1993. Taken from Fig.1 of Meyer et al (2000).