Interstellar Matter

Figure 1.1: Multiphases of the interstellar medium. The temperature and number density of gaseous objects of the interstellar medium in our Galaxy are summarized. Originally made by Myers (1978), reconstructed by Saigo (2000).

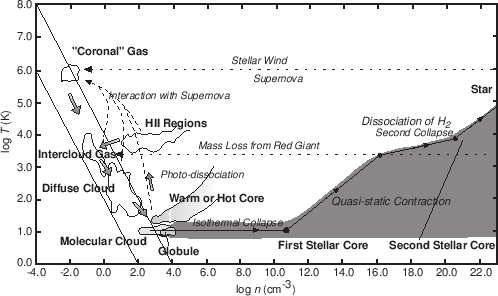Figure 1.1 shows the temperature and number density of gaseous objects in our Galaxy. Cold interstellar medium forms molecular clouds ($T\sim 10$K) and diffuse clouds ($T\sim 100$K). Warm interstellar medium $10^3{\rm K}\mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$... ...ox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10^4{\rm K}$ are thought to be pervasive (wide-spread). HII regions are ionized by the Ly continuum photons from the nearby early-type stars. There are coronal (hot but tenuous) gases with $T\sim 10^6$ K in the Galaxy, which are heated by the shock fronts of supernova remnants. Pressures of these gases are in the range of $10^2 {\rm K cm^{-3}} \mbox{\raisebox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.... ...ox{0.3ex}{$<$}\hspace{-1.1em} \raisebox{-0.7ex}{$\sim$}} 10^4 {\rm K cm^{-3}}$, except for the HII regions. This may suggest that gases are in the pressure equilibrium.

In this figure, a theoretical path from the molecular cloud core to the star is also shown. We will see the evolution more closely in Chapter 4.

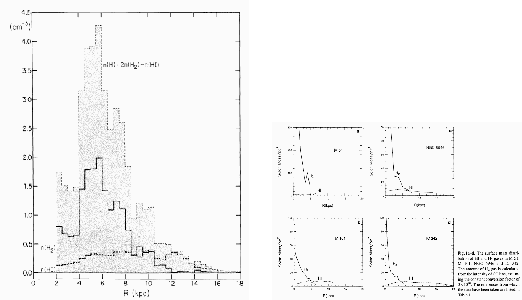
Globally, the molecular form of Hydrogen H$_2$ is much abundant inside the Solar circle, while the atomic hydrogen H${\sc I}$ is more abundant than molecular H$_2$ in the outer Galaxy. In Figure 1.2 (left), the radial distributions of molecular and atomic gases are shown. The right panel shows similar distributions for four typical external galaxies (M51, M101, NGC6946, and IC342). This indicates these distributions are similar with each other. HI is distributed uniformly, while H$_2$ density increases greatly reaching the galaxy center. In other words, only in the region where the total (HI+H$_2$) density exceeds some critical value, H$_2$ molecules are distributed.

Figure 1.2: Radial distribution of H$_2$ (solid line) and HI (dashed line) gas density. (Left:) our Galaxy. Converting from CO antenna temperature to H$_2$ column deity, $n({\rm CO})/n({\rm H_2})=6\times 10^{-5}$ is assumed. Taken from Gordon & Burton (1976). (Right:) Radial distribution of H$_2$ and HI gas for external galaxies. The conversion factor is assumed constant $X({\rm H_2/CO})=3\times 10^{20} {\rm H_2/K km s^{-1}}$. Taken from Honma et al (1995). About the $X$-factor refer to the appendix F.